题目内容
6.已知函数f(x)=$\frac{1}{{2}^{x}-1}$+1.(1)求函数的定义域;
(2)若f(x)>2x,求实数x的取值范围.
分析 (1)由式子有意义可得2x-1≠0,解不等式可得定义域为;
(2)原不等式可化为$\frac{1}{{2}^{x}-1}$>2x-1,整理可得$\frac{{2}^{x}({2}^{x}-2)}{{2}^{x}-1}$<0,可得1<2x<2,由指数函数可得.
解答 解:(1)由式子有意义可得2x-1≠0,解得x≠0,
∴已知函数的定义域为{x|x≠0};
(2)∵f(x)>2x,∴$\frac{1}{{2}^{x}-1}$+1>2x,
∴$\frac{1}{{2}^{x}-1}$>2x-1,即$\frac{1}{{2}^{x}-1}$-(2x-1)>0,
通分可得$\frac{1-({2}^{x}-1)^{2}}{{2}^{x}-1}$>0即$\frac{{2}^{x}({2}^{x}-2)}{{2}^{x}-1}$<0,
解得1<2x<2,解得0<x<1.
点评 本题考查分式不等式和指数不等式,涉及函数的定义域,属基础题.

练习册系列答案
相关题目
16.函数y=|x+1|+1的图象是( )
| A. | 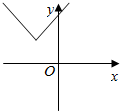 | B. |  | C. | 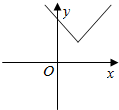 | D. |  |