题目内容
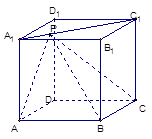
如图,四棱锥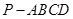 的底面
的底面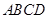 为矩形,且
为矩形,且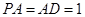 ,
,
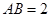 ,
,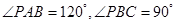 ,(Ⅰ)平面
,(Ⅰ)平面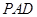 与平面
与平面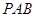 是否垂直?并说明理由;(Ⅱ)求直线
是否垂直?并说明理由;(Ⅱ)求直线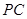 与平面
与平面 所成角的正弦值.
所成角的正弦值. 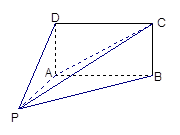
 的底面
的底面 为矩形,且
为矩形,且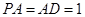 ,
,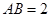 ,
,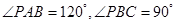 ,(Ⅰ)平面
,(Ⅰ)平面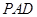 与平面
与平面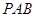 是否垂直?并说明理由;(Ⅱ)求直线
是否垂直?并说明理由;(Ⅱ)求直线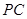 与平面
与平面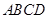 所成角的正弦值.
所成角的正弦值. 
(I)略
(Ⅱ)直线PC与平面ABCD所成角的正弦值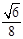
(Ⅱ)直线PC与平面ABCD所成角的正弦值
本试题主要是考查了立体几何中的面面垂直的证明,以及线面角的求解的综合运用
(1)根据面面垂直的判定定理,得到结论。关键是证明DA垂直于平面PAB。
(2)在平面PAB内,过点P作PE⊥AB,垂足为E,则PE⊥平面ABCD,连结EC,
则∠PCE为直线PC与平面ABCD所成的角,作出角,证明求解。
(1)根据面面垂直的判定定理,得到结论。关键是证明DA垂直于平面PAB。
(2)在平面PAB内,过点P作PE⊥AB,垂足为E,则PE⊥平面ABCD,连结EC,
则∠PCE为直线PC与平面ABCD所成的角,作出角,证明求解。

练习册系列答案
相关题目
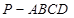 中,
中,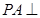 平面
平面 ,
,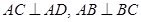 ,
,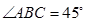 ,
,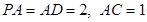 .
.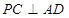 ;
; 的正弦值;
的正弦值;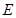 为棱
为棱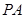 上的点,满足异面直线
上的点,满足异面直线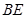 与
与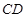 所成的角为
所成的角为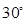 ,求
,求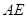 的长.
的长.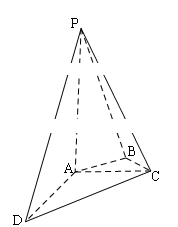

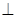 A1D;
A1D;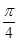 。
。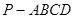 中,
中,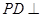 平面
平面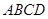 ,
,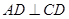 ,
,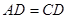 ,
,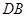 平分
平分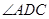 ,
,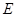 为
为 的中点.
的中点.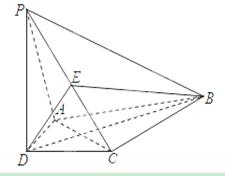
 平面
平面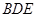 ;
;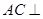 平面
平面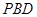 .
.
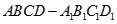 中,平面
中,平面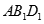 和平面
和平面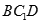 的位置关系为
的位置关系为 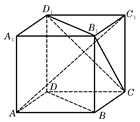
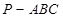 中,
中,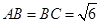 ,平面
,平面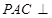 平面
平面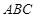 ,
,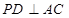 于点
于点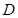 ,
, 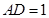 ,
,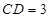 ,
,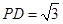 .
.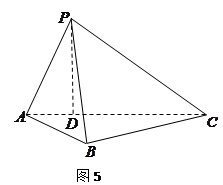
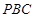 为直角三角形;
为直角三角形;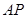 与平面
与平面