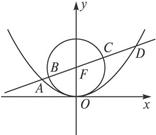
题目内容
若曲线
 的焦点F恰好是曲线
的焦点F恰好是曲线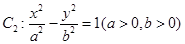 的右焦点,且
的右焦点,且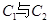 交点的连线过点F,则曲线
交点的连线过点F,则曲线 的离心率为
的离心率为

 的焦点F恰好是曲线
的焦点F恰好是曲线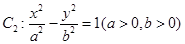 的右焦点,且
的右焦点,且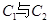 交点的连线过点F,则曲线
交点的连线过点F,则曲线 的离心率为
的离心率为A. | B.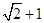 | C. | D. |
B
试题分析:抛物线与双曲线交于A(
 )、B(
)、B( )两点,则:
)两点,则:AB=
 +p
+p又A(c,
 ),B(c,-
),B(c,- ),c=
),c=
则2
 =2c+2c,所以
=2c+2c,所以 =2c,b²=2ac,由
=2c,b²=2ac,由 得
得c²-a²-2ac=0
(
 )²-2(
)²-2( )-1=0
)-1=0解得:e=
 =
=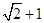 ,故选B。
,故选B。点评:基础题,结合图形特征,通过构建a,c的方程求得了离心率。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
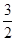 ),离心率为
),离心率为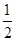 .
.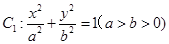 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆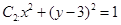 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为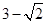 的直线
的直线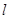 恰好与圆
恰好与圆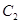 相切.
相切.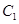 的离心率;
的离心率;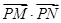 的最大值为49,求椭圆C
的最大值为49,求椭圆C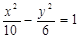 的焦点坐标是 ( )
的焦点坐标是 ( ) 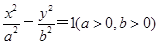 的一条渐近线的倾斜角为
的一条渐近线的倾斜角为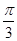 ,离心率为
,离心率为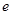 ,则
,则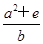 的最小值为( )
的最小值为( ) 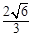
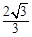
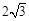
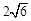
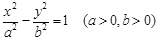 上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为
上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为
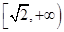
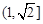

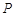 是椭圆
是椭圆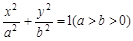 上的一动点,且
上的一动点,且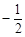 ,则椭圆离心率为
,则椭圆离心率为 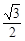
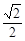
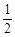
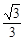
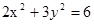 有两个交点 ( )
有两个交点 ( )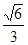 <k<
<k<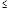 k
k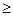
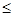 —
—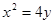 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆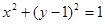 于点A、B、C、D,则
于点A、B、C、D,则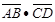 的值是( )
的值是( )