题目内容
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分X的分布列及数学期望EX.
| 3 |
| 4 |
| 2 |
| 3 |
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分X的分布列及数学期望EX.
分析:(I)设“该射手恰好命中两次”为事件A,分为两种情况:一种是两次射向甲靶都命中而向乙靶射击一次没有命中,其概率为
×
×(1-
);另一种是两次射向甲靶只有命中一次而向乙靶射击一次命中,其概率为
×
×(1-
)×
,相加即可得出.
(II)由题意可得:X=0,1,2,3,4.P(X=0)利用相互独立事件的概率计算公式即可得出;P(X=1)两次射向甲靶只有命中一次而向乙靶射击一次没有命中;P(X=2)一种是两次射向甲靶都命中而向乙靶射击一次没有命中,另一种是两次射向甲靶都没有命中而向乙靶射击一次命中;P(X=3)是两次射向甲靶只有命中一次而向乙靶射击一次命中;P(X=4)表示3次射击都命中.分别利用相互独立事件和互斥事件的概率计算公式计算出概率即可.
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| C | 1 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
(II)由题意可得:X=0,1,2,3,4.P(X=0)利用相互独立事件的概率计算公式即可得出;P(X=1)两次射向甲靶只有命中一次而向乙靶射击一次没有命中;P(X=2)一种是两次射向甲靶都命中而向乙靶射击一次没有命中,另一种是两次射向甲靶都没有命中而向乙靶射击一次命中;P(X=3)是两次射向甲靶只有命中一次而向乙靶射击一次命中;P(X=4)表示3次射击都命中.分别利用相互独立事件和互斥事件的概率计算公式计算出概率即可.
解答:解:(I)设“该射手恰好命中两次”为事件A,则P(A)=
×
×(1-
)+
×
×(1-
)×
=
=
.
(II)由题意可得:X=0,1,2,3,4.
P(X=0)=(1-
)2×(1-
)=
;
P(X=1)=
×
×(1-
)×(1-
)=
;
P(X=2)=(
)2×(1-
)+(1-
)2×
=
;
P(X=3)=
×
×(1-
)×
=
;
P(X=4)=(
)2×
=
.
∴E(X)=0×
+1×
+2×
+3×
+4×
=
.
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| C | 1 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 21 |
| 48 |
| 7 |
| 16 |
(II)由题意可得:X=0,1,2,3,4.
P(X=0)=(1-
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 48 |
P(X=1)=
| C | 1 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 6 |
| 48 |
P(X=2)=(
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 11 |
| 48 |
P(X=3)=
| C | 1 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 12 |
| 48 |
P(X=4)=(
| 3 |
| 4 |
| 2 |
| 3 |
| 18 |
| 48 |
∴E(X)=0×
| 1 |
| 48 |
| 6 |
| 48 |
| 11 |
| 48 |
| 12 |
| 48 |
| 18 |
| 48 |
| 17 |
| 6 |
点评:本题考查了相互独立事件和互斥事件的概率计算公式、分类讨论的思想方法等基础知识与基本方法,属于难题.

练习册系列答案
相关题目
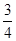 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。
,每命中一次得2分,没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。