Question

现有甲、乙两个靶。某射手向甲靶射击一次，命中的概率为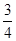，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为,每命中一次得2分，没有命中得0分。该射手每次射击的结果相互独立。假设该射手完成以上三次射击。

（Ⅰ）求该射手恰好命中一次的概率；

（Ⅱ）求该射手的总得分X的分布列及数学期望EX.

 

Answer 1

【答案】

（1）

（2）

X	0	1	2	3	4	5
P

EX=0×+1×+2×+3×+4×+5×=.

【解析】

试题分析：解：（Ⅰ）；

（Ⅱ）的可能取值为：0,1,2,3,4,5

,

X	0	1	2	3	4	5
P

EX=0×+1×+2×+3×+4×+5×=.

考点：独立事件概率公式运用

点评：主要是考查了分布列的求解和运用，以及独立事件概率的乘法公式，属于基础题。