题目内容
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(I)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量 的分布列和数学期望.
的分布列和数学期望.
【解析】(I) 、
、 可能的取值为
可能的取值为 、
、 、
、 ,…………………1分
,…………………1分
 ,
, ,
,
 ,且当
,且当 或
或 时,
时, .
.
因此,随机变量 的最大值为
的最大值为 …………………………4分
…………………………4分
有放回摸两球的所有情况有 种
种
 ………6分
………6分
(Ⅱ) 的所有取值为
的所有取值为 .
.
 时,只有
时,只有 这一种情况.
这一种情况.
 时,有
时,有 或
或 或
或 或
或 四种情况,
四种情况,
 时,有
时,有 或
或 两种情况.
两种情况.
 ,
, ,
, …………………………8分
…………………………8分
|
|
|
|
|
|
|
|
|
|
|
|
则随机变量 的分布列为:
的分布列为:
………………10分
因此,数学期望 …………………12分
…………………12分

练习册系列答案
相关题目
一个算法的程序框图如图所示,如果输入的x的值为2014,则输出的i的结果为( )

|
| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
设x,y满足约束条件 ,若目标函数z=ax+by(a>0,b>0)的最大值为12,则
,若目标函数z=ax+by(a>0,b>0)的最大值为12,则 +
+ 的最小值为( )
的最小值为( )
|
| A. | 4 | B. |
| C. | 1 | D. | 2 |




 )的部分图象,点A为函数f(x)在y轴右侧的第一个零点,点B在函数f(x)图象上,它的纵坐标为1,直线AB的倾斜角等于____.
)的部分图象,点A为函数f(x)在y轴右侧的第一个零点,点B在函数f(x)图象上,它的纵坐标为1,直线AB的倾斜角等于____.


 .
. ,若曲线
,若曲线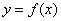 在点
在点 处的切线方程为
处的切线方程为 ,则
,则 .
. 的焦点
的焦点 直线与
直线与 交于
交于 两点.
两点.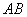 中点
中点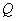 的轨迹方程;
的轨迹方程; 是抛物线
是抛物线 与抛物线C的准线
与抛物线C的准线 分别交于点
分别交于点 ,
, 的值.
的值.