题目内容

17．若tanα=2．
求（1）$\frac{2sinα-cosα}{sinα+2cosα}$；
（2）2sin2x-sinxcosx+cos2x．

分析 由条件利用同角三角函数的基本关系，求得要求式子的值．

解答 解：（1）∵tanα=2，∴$\frac{2sinα-cosα}{sinα+2cosα}=\frac{2tanα-1}{tanα+2}=\frac{3}{4}$．
（2）$2{sin^2}x-sinxcosx+{cos^2}x=\frac{{2{{sin}^2}x-sinxcosx+{{cos}^2}x}}{{{{sin}^2}x+{{cos}^2}x}}=\frac{{2{{tan}^2}x-tanx+1}}{{{{tan}^2}x+1}}=\frac{8-2+1}{4+1}=\frac{7}{5}$．

点评 本题主要考查同角三角函数的基本关系的应用，属于基础题．

练习册系列答案
相关题目
7．设α，β为两个不重合的平面，m，n为两条不重合的直线，给出下列四个命题：
①若m⊥n，m⊥α，n?α，则n∥α；
②若m⊥n，m∥α，n∥β，则α⊥β；
③若α⊥β，α∩β=m，n?α，n⊥m则n⊥β；
④若n?α，m?β，α与β相交且不垂直，则n与m一定不垂直．
其中，所有真命题的序号是①③．
8．已知M（x0，y0）是双曲线x2-$\frac{{y}^{2}}{2}$=1上的一点，F1，F2为C的两个焦点，若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$＜0，则y0的取值范围为（　　）
A．（-$\frac{\sqrt{6}}{3}$，$\frac{\sqrt{6}}{3}$）B．（-$\frac{2\sqrt{6}}{3}$，$\frac{2\sqrt{6}}{3}$）C．（-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$）D．（-$\frac{2\sqrt{3}}{3}$，$\frac{2\sqrt{3}}{3}$）
5．已知函数f（log2x）=x-$\frac{1}{x}$
（1）求函数f（x）的表达式，并说明函数的单调性、奇偶性（无需证明）；
（2）设集合A=$\{x|x=sinθ+cosθ，θ∈（-\frac{π}{2}，0）\}$，若函数y=f（x）（x∈A），且f（1-m）+f（1-m2）＜0，求实数 m的取值范围；
（3）若不等式2tf（2t）+mf（t）≥0对于t∈[1，2]恒成立，求实数 m的取值范围．
12．已知O是△ABC所在平面内一点，D为BC边中点．
（1）若点O满足$2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow 0$，求证：$\overrightarrow{AO}=\overrightarrow{OD}$；
（2）已知E为AC边中点，O在线段DE上，且满足$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$，△BOC的面积为2，求△ABC的面积．
2．已知曲线y=x+lnx在点（1，1）处的切线与曲线y=ax2+（a+2）x+l相切．求不等式x2-（a+l）x+a≤0的解集．
9．6本相同的数学书和3本不相同的语文书分给9个人，每人1本，共有不同分法（　　）
A．C${\;}_{9}^{3}$B．A${\;}_{9}^{3}$C．A${\;}_{9}^{6}$D．A${\;}_{9}^{3}$•A${\;}_{3}^{3}$
6．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（$\sqrt{2}$，1），且焦点为F1（-$\sqrt{2}$，0）
（Ⅰ）求椭圆C的方程；
（Ⅱ）当过点P（4，0）的动直线l与椭圆C相交于两不同点A，B时，在线段AB上取点Q，满足$\frac{|\overrightarrow{AP}|}{|\overrightarrow{PB}|}$=$\frac{|\overrightarrow{AQ}|}{|\overrightarrow{QB}|}$，证明：点Q总在某定直线上．
7．已知某空间几何体的三视图如图所示，则该几何体的体积为（　　）
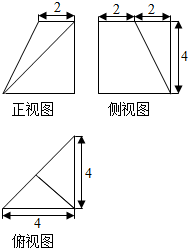
A．$\frac{16}{3}$B．$\frac{80}{3}$C．$\frac{40}{3}$D．40

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网