题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,x<0}\\{-\frac{1}{x},x>0}\end{array}\right.$的图象上存在不同的两点A,B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是(-2,$\frac{1}{4}$).分析 先根据导数的几何意义写出函数f(x)在点A、B处的切线方程,再利用两直线重合的充要条件:斜率相等且纵截距相等,列出关系式,从而得出a=$\frac{1}{4}$(t4-2t2-8t+1),判断单调性,可得出a的取值范围.
解答 解:当x<0时,f(x)=x2+x+a的导数为f′(x)=2x+1;
当x>0时,f(x)=-$\frac{1}{x}$的导数为f′(x)=$\frac{1}{{x}^{2}}$,
设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2,
当x1<x2<0,或0<x1<x2时,f′(x1)≠f′(x2),故x1<0<x2,
当x1<0时,函数f(x)在点A(x1,f(x1))处的切线方程为:
y-(x12+x1+a)=(2x1+1)(x-x1);
当x2>0时,函数f(x)在点B(x2,f(x2))处的切线方程为y+$\frac{1}{{x}_{2}}$=$\frac{1}{{{x}_{2}}^{2}}$(x-x2).
两直线重合的充要条件是$\frac{1}{{{x}_{2}}^{2}}$=2x1+1①,-$\frac{2}{{x}_{2}}$=-x12+a②,
由①及x1<0<x2得0<$\frac{1}{{x}_{2}}$<1,由①②令t=$\frac{1}{{x}_{2}}$,则0<t<1,
且a=$\frac{1}{4}$(t4-2t2-8t+1),导数为a′=t3-t-2,且a′<0在(0,1)恒成立,
则函数a在(0,1)为减函数,
∴-2<a<$\frac{1}{4}$,
故答案为:(-2,$\frac{1}{4}$).
点评 本题主要考查了导数的几何意义等基础知识,考查了推理论证能力、运算能力、创新意识,考查了函数与方程、分类与整合、转化与化归等思想方法.

 阅读快车系列答案
阅读快车系列答案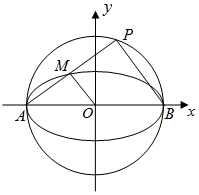 已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.
已知椭圆C的中心在原点,焦点在x轴上,离心率$e=\frac{{\sqrt{3}}}{2}$.且经过点(0,1),C与x轴交于A,B两点,以AB为直径的圆记为C1,P是C1上的异于A,B的点.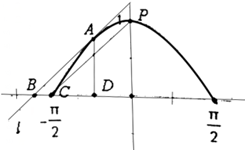 直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.
直线l与函数y=cosx(x∈[-$\frac{π}{2}$,$\frac{π}{2}$])图象相切于点A,且l∥CP,C(-$\frac{π}{2}$,0),P为图象的极值点,l与x轴交点为B,过切点A作AD⊥x轴,垂足为D,则$\overrightarrow{BA}•\overrightarrow{BD}$=$\frac{{π}^{2}-4}{4}$.