题目内容
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且![]() ,E是OC的中点。
,E是OC的中点。
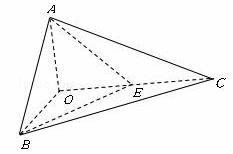
(1)求O点到面ABC的距离;
(2)求异面直线BE与AC所成角的余弦值;
(3)求二面角![]() 的余弦值。
的余弦值。
解:(1)取BC的中点D,连AD、OD
∵OB=OC,则OD⊥BC、AD⊥BC,
∴BC⊥面OAD,过O点作OH⊥AD于H,
则OH⊥面ABC,OH的长就是所要求的距离![]() 。
。
∵OA⊥OB、OA⊥OC,
∴OA⊥面OBC,则OA⊥OD。
![]() ,在直角三角形OAD中,有
,在直角三角形OAD中,有![]() 。
。
(另解:由![]() 知,
知,![]() 。)
。)
(2)取OA的中点M,连EM、BM,则EM∥AC,∠BEM是异面直线BE与AC所成的角。求得:![]() ,
,![]() 。
。
cos∠BEM=![]() 。
。
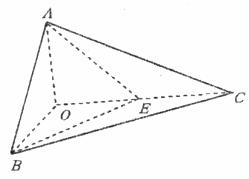
(3)连结CH并延长交AB于F,连结OF、EF。
∵OC⊥面OAB,∴OC⊥AB。又∵OH⊥面ABC,∴CF⊥AB,EF⊥AB,
则∠EFC就是所求二面角的平面角,作EG⊥CF于G,则
![]() ,
,
在直角三角形OAB中,![]() ,
,
在直角三角形OEF中,![]() ,
,
Sin∠EFG=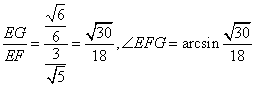 (或表示为
(或表示为![]() )
)
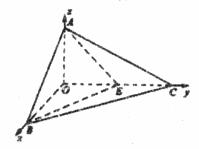
方法二:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系。

练习册系列答案
相关题目
 如图,已知三棱锥O-ABC中,
如图,已知三棱锥O-ABC中,| OA |
| a |
| OB |
| b |
| OC |
| c |
| AG |
A、
| ||||||||||
B、-
| ||||||||||
C、
| ||||||||||
D、-
|
 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=2,OC=4,E是OC的中点,求二面角E-AB-C的余弦值.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=2,OC=4,E是OC的中点,求二面角E-AB-C的余弦值.