题目内容
一次单元测试由20个选择题构成,每个选择题有4个选项,其中仅有一个选项正确,每题选对得5分,不选或选错不得分,满分得100分.学生甲选对任意一题的概率为0.9,学生乙则在测试中对每题都从各选项中随机地选择一个,分别求学生甲和学生乙在这次测试中成绩的均值.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:
分析:设学生甲和学生乙在这次测试中选对的题数分别为X1和X2,由题意知X1~B(20,0.9),X2~B(20,0.25),学生甲和学生乙在这次测试中的成绩分别为5X1和5X2,由此能求出学生甲和学生乙在这次测试中的成绩的均值.
解答:
解:设学生甲和学生乙在这次测试中选对的题数分别为X1和X2,
由题意知X1~B(20,0.9),X2~B(20,0.25),
∴EX1=20×0.9=18,EX2=20×0.25=5,
学生甲和学生乙在这次测试中的成绩分别为5X1和5X2,
∴学生甲和学生乙在这次测试中的成绩的均值分别为:
E(5X1)=5EX1=5×18=90,
E(5X2)=5EX2=5×5=25.
由题意知X1~B(20,0.9),X2~B(20,0.25),
∴EX1=20×0.9=18,EX2=20×0.25=5,
学生甲和学生乙在这次测试中的成绩分别为5X1和5X2,
∴学生甲和学生乙在这次测试中的成绩的均值分别为:
E(5X1)=5EX1=5×18=90,
E(5X2)=5EX2=5×5=25.
点评:本题考查离散型随机变量的数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
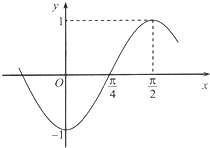 已知函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)部分图象如图所示.
已知函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)部分图象如图所示. 如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.
如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.