题目内容
20.设函数$f(x)=\left\{\begin{array}{l}{x^2},\;x≥a\\-x,\;x<a.\end{array}\right.$如果f(1)=1,那么a的取值范围是(-∞,1].分析 当a≥1时,f(1)=12=1,成立;当a<1时,f(1)=12=1,成立.由此能求出a的取值范围.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}{x^2},\;x≥a\\-x,\;x<a\end{array}\right.$,f(1)=1,
∴当a≥1时,f(1)=12=1,成立;
当a<1时,f(1)=12=1,成立.
∴a≤1,即a的取值范围是(-∞,1].
故答案为:(-∞,1].
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.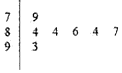 如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
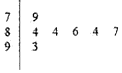 如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )
如图是2016年某学生进行舞蹈比赛环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和众数依次是( )| A. | 85.84 | B. | 84.85 | C. | 85.87 | D. | 84.86 |
15.用二分法找函数f(x)=2x+3x-7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( )
| A. | (0,1) | B. | (0,2) | C. | (2,3) | D. | (2,4) |
 满足
满足 ,且
,且 都是正数,则
都是正数,则 的最大值为 ( )
的最大值为 ( ) B.
B. C.
C. D.
D.