题目内容
在120°的二面角α-l-β内有一点P,P在平面α、β内的射影A、B分别落在半平面αβ内,且PA=3,PB=4,则P到l的距离为分析:由已知中在120°的二面角α-l-β内有一点P,P在平面α、β内的射影A、B分别落在半平面αβ内,且PA=3,PB=4,我们易求出AB的长,利用四点共圆及圆周角定理的推理,我们易得到P到l的距离即为△PAB的外接圆直径,利用正弦定理,求出圆的直径即可得到答案.
解答:解:∵在120°的二面角α-l-β内有一点P,
P在平面α、β内的射影A、B分别落在半平面αβ内,
∴∠APB=60°
又∵PA=3,PB=4,
∴AB=
=
,
而P到l的距离即为△PAB的外接圆直径,
由正弦定理得2R=
=
=
,
故答案为:
.
P在平面α、β内的射影A、B分别落在半平面αβ内,
∴∠APB=60°
又∵PA=3,PB=4,
∴AB=
| PA2+PB2-2PA•PB•cos∠APB |
| 13 |
而P到l的距离即为△PAB的外接圆直径,
由正弦定理得2R=
| AB |
| sin∠APB |
| ||||
|
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查的知识点是空间点、线、面之间的距离计算,二面角的平面角及求法,其中将空间问题转化为平面问题后,得到P到l的距离即为△PAB的外接圆直径是解答本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
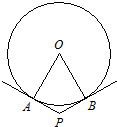 (2008•普陀区一模)在120°的二面角内放一个半径为6的球,使球与两个半平面各只有一个公共点(其过球心且垂直于二面角的棱的直截面如图所示),则这两个公共点AB之间的球面距离为
(2008•普陀区一模)在120°的二面角内放一个半径为6的球,使球与两个半平面各只有一个公共点(其过球心且垂直于二面角的棱的直截面如图所示),则这两个公共点AB之间的球面距离为