题目内容
(2008•和平区三模)在120°的二面角内放一个半径为6的球,与两个半平面各有且仅有一个公共点,则这两点间的球面距离是
2π
2π
.分析:作出经过球心且与二面角的棱垂直的截面,得到如图所示的平面图形.由题意,可得该四边形中∠APB=120°,OA⊥AP且OB⊥PB,从而算出∠AOB=60°,再利用球面距离计算公式即可算出答案.
解答:解:作出过球心且与二面角的棱垂直的截面,得到如图所示的平面图形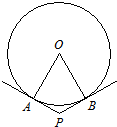
设球心为O,两个切点分别为A、B,平面AOB交二面角的棱于点P
由题意可得∠APB=120°,连结OA、OB,
根据切线的性质得:OA⊥AP且OB⊥PB
∴四边形AOPB中,∠AOB=180°-120°=60°
因此,A、B之间的球面距离为l=
×2πR=
×π×6=2π
故答案为:2π

设球心为O,两个切点分别为A、B,平面AOB交二面角的棱于点P
由题意可得∠APB=120°,连结OA、OB,
根据切线的性质得:OA⊥AP且OB⊥PB
∴四边形AOPB中,∠AOB=180°-120°=60°
因此,A、B之间的球面距离为l=
| 1 |
| 6 |
| 1 |
| 3 |
故答案为:2π
点评:本题给出张角为120度的二面角的一个内切球的问题,求两点间的球面距离,着重考查了圆的切线性质、二面角的定义和球面距离计算等知识,属于基础题.

练习册系列答案
相关题目
 (2008•和平区三模)如图,在△ABC中,∠ABC=∠ACB=30°,AB,AC边上的高分别为CD,BE,则以B,C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为
(2008•和平区三模)如图,在△ABC中,∠ABC=∠ACB=30°,AB,AC边上的高分别为CD,BE,则以B,C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为