题目内容
给出下列四个命题:
①有两个侧面是矩形的四棱柱是直四棱柱;
②若f(x)是单调函数,则f(x)与它的反函数f -1(x)具有相同的单调性;
③若两平面垂直相交于直线m,则过一个平面内一点垂直于m的直线就垂直于另一平面;
④在120°的二面角内放一个半径为6的球,使它与两个半平面各有且仅有一个公共点,则球心到这个二面角的棱的距离是2
.其中,不正确命题的序号为
①有两个侧面是矩形的四棱柱是直四棱柱;
②若f(x)是单调函数,则f(x)与它的反函数f -1(x)具有相同的单调性;
③若两平面垂直相交于直线m,则过一个平面内一点垂直于m的直线就垂直于另一平面;
④在120°的二面角内放一个半径为6的球,使它与两个半平面各有且仅有一个公共点,则球心到这个二面角的棱的距离是2
| 3 |
①
①
.分析:①当两个侧面是矩形且相邻时,四棱柱是直四棱柱;当两个侧面是矩形且不相邻时,四棱柱不是直四棱柱;
②若f(x)是单调函数,必然存在反函数,根据互为反函数的两个函数关于y=x对称,故具有相同的单调性;
③根据面面垂直的性质定理可知,结论正确;
④由题意可得,∠APB=120°,根据切线的性质可得,OA⊥AP,OB⊥PB,从而可得∠AOB=60°,从而可求球心到这个二面角的棱的距离
②若f(x)是单调函数,必然存在反函数,根据互为反函数的两个函数关于y=x对称,故具有相同的单调性;
③根据面面垂直的性质定理可知,结论正确;
④由题意可得,∠APB=120°,根据切线的性质可得,OA⊥AP,OB⊥PB,从而可得∠AOB=60°,从而可求球心到这个二面角的棱的距离
解答:解:①当两个侧面是矩形且相邻时,四棱柱是直四棱柱;当两个侧面是矩形且不相邻时,四棱柱不是直四棱柱,故①错;
②若f(x)是单调函数,必然存在反函数,根据互为反函数的两个函数关于y=x对称,可知②正确;
③根据面面垂直的性质定理可知,若两平面垂直相交于直线m,则过一个平面内一点垂直于m的直线就垂直于另一平面,故正确;
④由题意可得,∠APB=120°,连接OA,OB,则根据切线的性质可得,OA⊥AP,OB⊥PB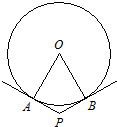
∴∠AOB=60°
∴球心到这个二面角的棱的距离是OP=2
,故正确.
故答案为:①
②若f(x)是单调函数,必然存在反函数,根据互为反函数的两个函数关于y=x对称,可知②正确;
③根据面面垂直的性质定理可知,若两平面垂直相交于直线m,则过一个平面内一点垂直于m的直线就垂直于另一平面,故正确;
④由题意可得,∠APB=120°,连接OA,OB,则根据切线的性质可得,OA⊥AP,OB⊥PB

∴∠AOB=60°
∴球心到这个二面角的棱的距离是OP=2
| 3 |
故答案为:①
点评:本题以命题为载体,考查立体几何中的概念与性质,解题时应一一判断,正确运用相关定理.

练习册系列答案
相关题目