题目内容
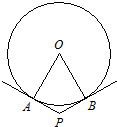（2008•普陀区一模）在120°的二面角内放一个半径为6的球，使球与两个半平面各只有一个公共点（其过球心且垂直于二面角的棱的直截面如图所示），则这两个公共点AB之间的球面距离为2π
2π
．分析：由题意可得，APB=120°，根据切线的性质可得，OA⊥AP，OB⊥PB，从而可得∠AOB=60°，根据AB球面距离公式l=α•r可求
解答：解：由题意可得，APB=120°
连接OA，OB，则根据切线的性质可得，OA⊥AP，OB⊥PB
∴∠AOB=60°
△AOB为等边三角形
AB之间的球面距离l=α•r=
×6=2π
故答案为：2π
连接OA，OB，则根据切线的性质可得，OA⊥AP，OB⊥PB
∴∠AOB=60°
△AOB为等边三角形
AB之间的球面距离l=α•r=
| π |
| 3 |
故答案为：2π
点评：本题主要考查了二面角的平面角的应用，球面距离的求解，属于基础试题
练习册系列答案
新思维寒假作业系列答案
相关题目
（2008•普陀区一模）一个圆柱形容器的轴截面尺寸如右图所示，容器内有一个实心的球，球的直径恰等于圆柱的高．现用水将该容器注满，然后取出该球（假设球的密度大于水且操作过程中水量损失不计），则球取出后，容器中水面的高度为
（2008•普陀区一模）如图，在直三棱柱ABC-A1B1C1中，CC1=AC=BC，∠ACB=90°，P是AA1的中点，Q是AB的中点．