Question

已知长方体ABCD-A₁B₁C₁D₁中，AB=，BC=AA₁=2，M是BD₁上的动点，M到A₁的距离为d₁，M到平面ABCD的距离为d₂，则d₁+d₂的最小值为__________.

Answer 1

答案：3【解析】本题考查空间直角坐标运算、向量共线以及求函数最值等知识.如图,以,D₁为坐标原点,分别以射线D_lA_l、D_lC₁、DD₁为x轴,y轴、z轴建立空间直角坐标系.

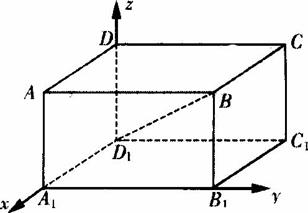
则A_l(2,0,0),D_l(0,0,0),B(2,2,2),设M

则=(x,y,z).M在BD₁上,所以

故M(2λ,2,2λ).

所以d_l+d₂==

设f()=2(0≤λ≤1).则f′(λ)=

令f'′(λ)=0,解之得λ=0或λ=.因为λ∈[0,1],f(0)=4,

F()=3,f(1)=2.故当λ=,即当M在线段BD₁的中点时,d_l+d₂取得最小值3.