题目内容
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. | B. |
C. | D. |
B
解析试题分析:先有三视图得到几何体的形状及度量关系,利用棱锥的体积公式求出体积.解:由三视图可得几何体是四棱锥V-ABCD,其中面VCD⊥面ABCD;底面ABCD是边长为20cm的正方形;棱锥的高是20cm,由棱锥的体积公式得V= Sh=
Sh= ×20×20×20=
×20×20×20= cm3,故答案为B
cm3,故答案为B
考点:三视图
点评:三视图是新增考点,根据三张图的关系,可知几何体是正方体的一部分,是一个四棱锥.本题也可改编为求该几何体的外接球的表面积,则必须补全为正方体,增加了难度

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
半径为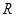 的半圆卷成一个圆锥,则它的体积为( ).
的半圆卷成一个圆锥,则它的体积为( ).
A.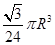 | B. | C. | D. |
已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则 ”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若
”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若 的中心为M,四面体内部一点O到四面体各面的距离都相等”,则
的中心为M,四面体内部一点O到四面体各面的距离都相等”,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
网格纸的小正方形边长为1,一个正三棱锥的左视图如图所示,则这个正三棱锥的体积为( )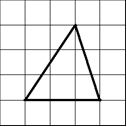
A.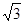 | B.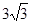 | C.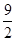 | D. |
 的棱长为1,动点P在此正方体的表面上运动,且
的棱长为1,动点P在此正方体的表面上运动,且 ,记点P的轨迹的长度为
,记点P的轨迹的长度为 ,则函数的图像
,则函数的图像


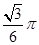
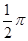
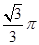
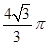
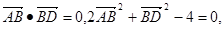 若将其沿BD折起,使平面ABD
若将其沿BD折起,使平面ABD 平面BDC则三棱锥A-BCD的外接球的表面积为:( )
平面BDC则三棱锥A-BCD的外接球的表面积为:( )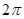






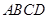 沿对角线
沿对角线 折成直二面角
折成直二面角 ,有如下四个结论:
,有如下四个结论: ⊥
⊥ 是等边三角形;③
是等边三角形;③ 与平面
与平面 所成的角为60°;④
所成的角为60°;④ 所成的角为60°.其中错误的结论是( )
所成的角为60°.其中错误的结论是( )