题目内容
四面体ABCD中，AC=BD，E，F分别为AD，BC的中点，且EF=
AC，∠BDC=90°，求证：BD⊥平面ACD．
| ||
| 2 |
证明：取CD的中点G，连接EG，FG，∵E，F分别为AD，BC的中点，
∴EG
AC；FG
BD，又AC=BD，∴FG=
AC，
∴在△EFG中，EG2+FG2=
AC2=EF2
∴EG⊥FG，∴BD⊥AC，又∠BDC=90°，即BD⊥CD，AC∩CD=C，
∴BD⊥平面ACD．
∴EG
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
| 1 |
| 2 |
| 1 |
| 2 |
∴在△EFG中，EG2+FG2=
| 1 |
| 2 |
∴EG⊥FG，∴BD⊥AC，又∠BDC=90°，即BD⊥CD，AC∩CD=C，
∴BD⊥平面ACD．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
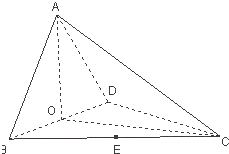如图，四面体ABCD中，O、E分别是BD、BC的中点，CA=CB=CD=BD=2，AB=AD=
已知O是△ABC内任意一点，连结AO，BO，CO并延长交对边于A′，B′，C′，则
=a, 
=b, 
=c,G为△BCD的重心，则
=__________.
= a，
= b，
= c，G∈平面ABC．则G为△ABC的重心的充分必要条件是
(a+b+c)；