题目内容
等差数列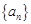 中,
中,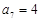 ,
,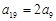 .
.
(1)求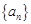 的通项公式;
的通项公式;
(2)设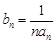 ,求数列
,求数列 的前
的前 项和
项和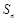 .
.
(1) (2)
(2)
解析试题分析:
(1)根据等差数列的通项公式,可知需要求出首项和公差,利用已知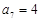 ,
,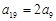 展开联立可得首项和公差,从而得到数列的通项公式.
展开联立可得首项和公差,从而得到数列的通项公式.
(2)将(1)中结果代入 ,根据其特点,分裂该通项为
,根据其特点,分裂该通项为 ,然后求和,可以抵消除去首项和末项的所有项,从而求得数列的和.
,然后求和,可以抵消除去首项和末项的所有项,从而求得数列的和.
试题解析:
(1)设等差数列 的公差为
的公差为 d,则
d,则 .
.
因为 ,所以
,所以 .
.
解得 .
.
所以 的通项公式为
的通项公式为 .
.
(2) .
.
所以 .
.
考点:等差数列求通项;裂项相消法求数列前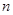 项和.
项和.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
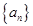 的前n项和为
的前n项和为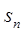 ,若
,若

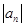 ,
, 。
。 的前n项和为
的前n项和为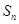 ,若
,若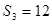 ,且
,且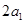 ,
,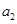 ,
,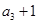 成等比数列,
成等比数列,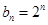 ,求数列
,求数列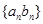 的前n项和
的前n项和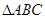 中,角
中,角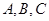 的对边分别为
的对边分别为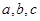 ,且
,且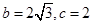 ,求
,求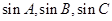 成等比数列,试判断
成等比数列,试判断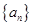 的前n项和为
的前n项和为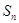 ,且满足条件
,且满足条件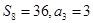
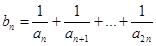 ,若对任意正整数
,若对任意正整数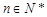 ,
, 恒成立,求
恒成立,求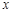 的取值范围.
的取值范围. 的等差数列,已知它的前10项和为
的等差数列,已知它的前10项和为 ,且a1,a2,a4 成等比数列.
,且a1,a2,a4 成等比数列.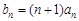 ,求数列
,求数列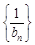 的前
的前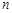 项和Tn .
项和Tn .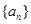 满足
满足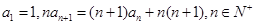
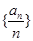 是等差数列;
是等差数列;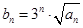 ,求数列
,求数列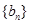 的前
的前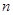 项和
项和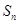
 的公差大于零的等差数列,已知
的公差大于零的等差数列,已知 ,
, .
. 是以函数
是以函数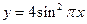 的最小正周期为首项,以
的最小正周期为首项,以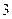 为公比的等比数列,求数列
为公比的等比数列,求数列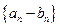 的前
的前 项和
项和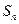 .
.