题目内容
在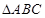 中,角
中,角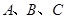 对边分别是
对边分别是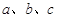 ,且满足
,且满足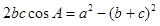 .
.
(Ⅰ)求角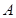 的大小;
的大小;
(Ⅱ)若 ,
,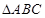 的面积为
的面积为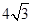 ;求
;求 .
.
(Ⅰ)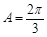 ;(Ⅱ)
;(Ⅱ)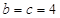 .
.
解析试题分析:(Ⅰ)利用余弦定理 得
得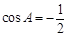 ,则
,则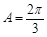 .(Ⅱ)利用三角形面积公式
.(Ⅱ)利用三角形面积公式 ,得出
,得出 ,而余弦定理
,而余弦定理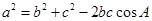 ,得出
,得出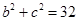 ,由上两式得出
,由上两式得出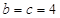 .
.
试题解析:(Ⅰ)由余弦定理得 ,代入
,代入 得
得 ,∴
,∴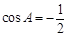 , ∵
, ∵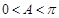 ,∴
,∴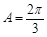
(Ⅱ) ,
,
解得: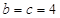 .
.
考点:1.向量数量积;2.余弦定理与三角形面积公式.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
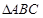 的内角A、B、C所对的边为
的内角A、B、C所对的边为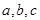 ,
,  ,
, 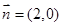 ,且
,且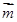 与
与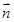 所成角为
所成角为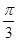 .
. 的取值范围.
的取值范围. 的内角
的内角 所对边的长分别为
所对边的长分别为 ,且有
,且有 .
.
 ,
, ,
, 为
为 的中点,求
的中点,求 的长.
的长. 中,内角
中,内角 对边分别为
对边分别为 ,
,
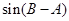 的值.
的值. 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 .
. 的值;
的值; ,求
,求 和
和 的值.
的值.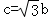 .
.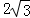 ,求a,b的值.
,求a,b的值. 中,
中, ,
, ,设
,设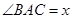 ,并记
,并记
 的解析式及其定义域;
的解析式及其定义域; ,若函数
,若函数 的值域为
的值域为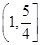 ,试求正实数
,试求正实数 的值
的值 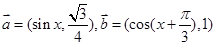 ,函数
,函数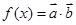 .
.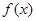 的最值和单调递减区间;
的最值和单调递减区间;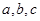 ,
,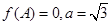 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.