Question

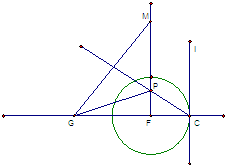如图，直线λ与半径为1的圆F相切于C．动点P到直线λ的距离为d，已知

|PF|

d

=

2

2

，且

2

3

≤d≤

3

2

．
（Ⅰ）建立适当的直角坐标系，求点P运动形成的轨迹方程；
（Ⅱ）若点G满足

GF

=2

FC

，点M满足

MP

=3

PF

且线段MG的垂直平分线经过P，求△PGF的面积．

Answer 1

考点：轨迹方程,正弦定理

专题：计算题,平面向量及应用,圆锥曲线的定义、性质与方程

分析：（1）利用两点的距离公式及点到直线的距离公式将已知几何条件用坐标表示，化简求出轨迹方程，注意求出定义域．
（2）利用已知条件的向量关系求出G为左焦点，利用中垂线的性质及椭圆的定义列出方程组，求出三角形PGF的三边长，利用勾股定理判断出三角形的性质，利用三角形的面积公式去求出三角形的面积．

解答： 解：（1）以CF所在直线为x轴，建立如图所示的直角坐标系，
设动点P的坐标为（x，y），F（1，0），直线λ：x=2
则|PF|=

(x-1)2+y2

，d=|2-x|，
则

(x-1)2+y2

|2-x|

=

2

2

，
化简得

x2

2

+y²=1
又

2

3

≤d=2-x≤

3

2

∴

1

2

≤x≤

4

3

，
即动点p的轨迹方程为

x2

2

+y²=1（

1

2

≤x≤

4

3

）；
（2）由已知，得|

FG

|=2|

FC

|=2，
∴G为左焦点
又∵

| PG |=| PM |=3| PF | | PG |+| PF |=2 2

，
∴

| PF |= 2 2 | PG |= 3 2 2

，
又∵|

GF

|=2，
∴|

PF

|²+|

GF

|²=|

PG

|²，
∴△PGF为直角三角形．
∴S△PFG=

1

2

|

PF

|•|

FG

|=

1

2

×

2

2

×2=

2

2

．

点评：本题考查求轨迹方程时，在化简方程时要注意同解变形，求出方程的定义域、考查解决焦点三角形问题常考虑利用圆锥曲线的定义．