题目内容
150° 弧度
三角函数y=sinx的最大值=
三角函数y=cosx的最小正周期是 .
三角函数y=sinx的最大值=
三角函数y=cosx的最小正周期是
考点:三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:先计算得150°=
×150°=
.由三角函数的图象和性质可求得y=sinx的最大值,y=cosx的最小正周期.
| π |
| 180 |
| 5π |
| 6 |
解答:
解:150°=
×150°=
.
由三角函数的图象和性质可知:y=sinx的最大值=1.
y=cosx的最小正周期是T=
=2π.
故答案为:
,1,2π
| π |
| 180 |
| 5π |
| 6 |
由三角函数的图象和性质可知:y=sinx的最大值=1.
y=cosx的最小正周期是T=
| 2π |
| 1 |
故答案为:
| 5π |
| 6 |
点评:本题主要考察了三角函数的周期性及其求法,三角函数的图象和性质,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
cos(
π)的值( )
| 13 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列命题中正确的是( )
| A、三角形的内角是第一象限角或第二象限角 | ||
| B、第一象限角是锐角 | ||
| C、第一象限角不是锐角 | ||
D、角α是第四象限角则有2kπ-
|
已知
和
是两个单位向量,夹角为
,则下面向量中与2
-
垂直的是( )
| e1 |
| e2 |
| π |
| 3 |
| e2 |
| e1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若抛物线y2=2px(p>0)上一点Q到准线和抛物线的对称轴的距离分别为10和6,则此点Q的横坐标为( )
| A、1 | B、9 | C、2 | D、1或9 |
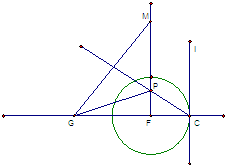 如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知