题目内容
已知函数f(x)=x+
,
(1)判定函数f(x)的奇偶性;
(2)讨论函数f(x)在区间(-∞,-1]上的单调性;
(3)求函数f(x)在区间[2,4]上的最值.
| 1 |
| x |
(1)判定函数f(x)的奇偶性;
(2)讨论函数f(x)在区间(-∞,-1]上的单调性;
(3)求函数f(x)在区间[2,4]上的最值.
考点:奇偶性与单调性的综合,函数单调性的判断与证明,函数单调性的性质,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据函数奇偶性的定义即可判定函数f(x)的奇偶性;
(2)根据函数单调性的定义即可讨论函数f(x)在区间(-∞,-1]上的单调性;
(3)利用函数单调性的性质求函数f(x)在区间[2,4]上的最值.
(2)根据函数单调性的定义即可讨论函数f(x)在区间(-∞,-1]上的单调性;
(3)利用函数单调性的性质求函数f(x)在区间[2,4]上的最值.
解答:
解:(1)函数的定义域为{x|x≠0},
则f(-x)=-x-
=-(x+
)=-f(x),则f(x)是奇函数.
(2)设x1<x2≤-1,
则f(x1)-f(x2)=x1+
-x2-
=(x1-x2)•
,
∵x1<x2≤-1,
∴x1-x2<0,x1x2>1,
则f(x1)-f(x2)<0,即f(x1)<f(x2),
则f(x)是单调增函数.
(3)由(2)可以证明函数f(x)在区间[2,4]上单调递增,
∴ymax=f(4)=4+
=
ymin=f(2)=2+
=
则f(-x)=-x-
| 1 |
| x |
| 1 |
| x |
(2)设x1<x2≤-1,
则f(x1)-f(x2)=x1+
| 1 |
| x1 |
| 1 |
| x2 |
| x1x2-1 |
| x1x2 |
∵x1<x2≤-1,
∴x1-x2<0,x1x2>1,
则f(x1)-f(x2)<0,即f(x1)<f(x2),
则f(x)是单调增函数.
(3)由(2)可以证明函数f(x)在区间[2,4]上单调递增,
∴ymax=f(4)=4+
| 1 |
| 4 |
| 17 |
| 4 |
ymin=f(2)=2+
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查函数奇偶性和单调性的判断和证明,利用定义法是解决本题的关键.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、三角形的内角是第一象限角或第二象限角 | ||
| B、第一象限角是锐角 | ||
| C、第一象限角不是锐角 | ||
D、角α是第四象限角则有2kπ-
|
若抛物线y2=2px(p>0)上一点Q到准线和抛物线的对称轴的距离分别为10和6,则此点Q的横坐标为( )
| A、1 | B、9 | C、2 | D、1或9 |
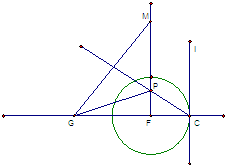 如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
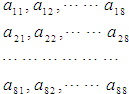 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=