题目内容

1．求过直线x+3y+7=0与3x-2y-12=0的交点，且圆心为（-1，1）的圆的方程．

分析 先求出过直线x+3y+7=0与3x-2y-12=0的交点，可得圆心坐标和半径，从而求得圆的标准方程．

解答 解：由$\left\{\begin{array}{l}{x+3y+7=0}\\{3x-2y-12=0}\end{array}\right.$，求得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$，故两条直线的交点为（2，-3），
故要求的圆的圆心为（-1，1），半径为$\sqrt{{（2+1）}^{2}{+（-3-1）}^{2}}$=5，
故要求的圆的方程为 （x+1）2+（y-1）2=25．

点评 本题主要考查求直线的交点坐标，圆的标准方程，求出半径，是解题的关键，属于基础题．

练习册系列答案
相关题目
11．一棱柱有10个顶点，且所有侧棱长之和为100，则其侧棱长为（　　）
A．10B．20C．5D．15
12．直线x+2y-2=0关于直线x=1对称的直线方程是（　　）
A．x-2y+1=0B．x+2y-1=0C．x-2y+5=0D．x-2y=0
9．已知抛物线C：y2=2px（p＞0）过点A（1，-2）．
（1）求抛物线C的标准方程；
（2）已知直线y=kx-1，当直线与抛物线有公共点时，求k的取值范围．
16．已知函数$f（x）=\frac{{{e^x}-a}}{{{e^x}+1}}$是奇函数．
（1）求实数a的值．
（2）判断f（x）在R上的单调性，并用定义证明．
（3）是否存在实数t，使不等式f（x-t）+f（x2-t2）≥0对一切x∈[1，2]恒成立？若存在，求出t的取值范围；若不存在，请说明理由．
6．在两个变量y与x的回归模型中，分别选择了4个不同的模型，它们的相关指数R2如下，其中拟合效果最好的模型是（　　）
A．模型1的相关指数R2为0.25B．模型2的相关指数R2为0.87
C．模型3的相关指数R2为0.50D．模型4的相关指数R2为0.97
13．设α，β是两个不同的平面，l是直线，以下命题不正确的是（　　）
A．若l∥α，α⊥β，则l∥βB．若l∥α，α∥β，则l∥β或l⊆β
C．若l⊥α，α∥β，则l⊥βD．若l⊥α，α⊥β，则l∥β或l⊆β
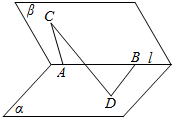10．如图，在二面角α-l-β的棱l上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB，若二面角α-l-β的大小为$\frac{π}{3}$，AB=AC=2，CD=$\sqrt{11}$，则BD=3．
11．已知抛物线y2=4px（p＞0）与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）有相同的焦点F，点A是两曲线的交点，且AF⊥x轴，则双曲线的离心率为$\sqrt{2}$+1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网