题目内容
一条双曲线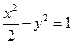 的左、右顶点分别为A1,A2,点
的左、右顶点分别为A1,A2,点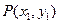 ,
,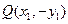 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。
(1)求直线A1P与A2Q交点的轨迹E的方程式;
(2)若过点H(0, h)(h>1)的两条直线l1和l2与轨迹E都只有一个交点,且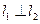 ,求h的值。
,求h的值。
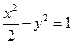 的左、右顶点分别为A1,A2,点
的左、右顶点分别为A1,A2,点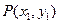 ,
,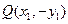 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。(1)求直线A1P与A2Q交点的轨迹E的方程式;
(2)若过点H(0, h)(h>1)的两条直线l1和l2与轨迹E都只有一个交点,且
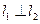 ,求h的值。
,求h的值。 ,
,
 故
故
 ,即
,即 。
。(2)设
 ,则由
,则由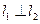 知,
知, 。
。将
 代入
代入 得
得 ,即
,即 ,
,由
 与E只有一个交点知,
与E只有一个交点知, ,即
,即 。
。同理,由
 与E只有一个交点知,
与E只有一个交点知, ,消去
,消去 得
得 ,即
,即 ,从而
,从而 ,即
,即 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左、右焦点,以坐标原点O为圆心,以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A,与y轴正半轴的交点为B,点A在y轴上的射影为H,且
的左、右焦点,以坐标原点O为圆心,以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A,与y轴正半轴的交点为B,点A在y轴上的射影为H,且
 的值.
的值.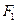 、
、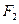 为双曲线C:
为双曲线C: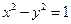 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠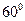 ,则P到x轴的距离为
,则P到x轴的距离为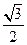
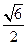
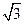
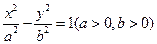 相交于B、D两点,且BD的中点为M(1.3)
相交于B、D两点,且BD的中点为M(1.3)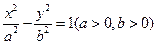 的右焦点为
的右焦点为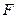 ,右准线与双曲线渐近线交于
,右准线与双曲线渐近线交于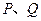 两点,如果
两点,如果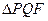 是直角三角形,则双曲线的离心率
是直角三角形,则双曲线的离心率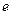 为 .
为 .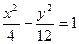 上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )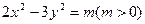 ,此双曲线的离心率为
,此双曲线的离心率为
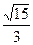
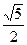
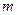 的值有关
的值有关 :
: 右支上的点
右支上的点 的切线
的切线 平分
平分 。现过原点作
。现过原点作 于
于 ,则
,则 等于( ▲ )
等于( ▲ )



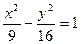 有共同的渐近线,并且过点A(
有共同的渐近线,并且过点A(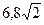 )的双曲线的标准方程为________________________.
)的双曲线的标准方程为________________________.