题目内容
给出命题p:方程
+
=1表示焦点在y轴上的椭圆;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.
(1)若命题p是真命题,求a的取值范围;
(2)如果命题“p∨q”为真,“p∧q”为假,求实数a的取值范围.
| x2 |
| a |
| y2 |
| 2-a |
(1)若命题p是真命题,求a的取值范围;
(2)如果命题“p∨q”为真,“p∧q”为假,求实数a的取值范围.
(1)若命题p为真,则有
解之得0<a<1,即实数a的取值范围为(0,1);
(2)若命题q为真,则有
△=(2a-3)2-4>0,解之得a<
或a>
∵命题“p∨q”为真,“p∧q”为假
∴p、q中一个为真命题,另一个为假命题,
①当p真q假时,
,得
≤a<1;
②当p假q真时,
,得a≤0或a≥
所以a的取值范围是(-∞,0]∪[
,1)∪[
,+∞).
|
解之得0<a<1,即实数a的取值范围为(0,1);
(2)若命题q为真,则有
△=(2a-3)2-4>0,解之得a<
| 1 |
| 2 |
| 5 |
| 2 |
∵命题“p∨q”为真,“p∧q”为假
∴p、q中一个为真命题,另一个为假命题,
①当p真q假时,
|
| 1 |
| 2 |
②当p假q真时,
|
| 5 |
| 2 |
所以a的取值范围是(-∞,0]∪[
| 1 |
| 2 |
| 5 |
| 2 |

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
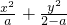 =1表示焦点在y轴上的椭圆;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.
=1表示焦点在y轴上的椭圆;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.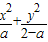 =1表示焦点在y轴上的椭圆;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.
=1表示焦点在y轴上的椭圆;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.