题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}{xln(1+x)+{x}^{2},x≥0}\\{-xln(1-x)+{x}^{2},x<0}\end{array}\right.$,若f(-a)+f(a)≤2f(1),则实数a的取值范围是( )| A. | (-∞,-1]∪[1,+∞) | B. | [-1,0] | C. | [0,1] | D. | [-1,1] |
分析 判断f(x)为偶函数,运用导数判断f(x)在[0,+∞)的单调性,则f(-a)+f(a)≤2f(1)转化为|a|≤1,解不等式即可得到a的范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{xln(1+x)+{x}^{2},x≥0}\\{-xln(1-x)+{x}^{2},x<0}\end{array}\right.$,
将x换为-x,函数值不变,即有f(x)图象关于y轴对称,
即f(x)为偶函数,有f(-x)=f(x),
当x≥0时,f(x)=xln(1+x)+x2的导数为f′(x)=ln(1+x)+$\frac{x}{1+x}$+2x≥0,
则f(x)在[0,+∞)递增,
f(-a)+f(a)≤2f(1),即为2f(a)≤2f(1),
可得f(|a|))≤f(1),可得|a|≤1,
解得-1≤a≤1.
故选:D.
点评 本题考查函数的奇偶性和单调性的应用:解不等式,注意运用导数判断单调性,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
18.设M为边长为4的正方形ABCD的边BC的中点,N为正方形区域内任意一点(含边界),则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最大值为( )
| A. | 32 | B. | 24 | C. | 20 | D. | 16 |
20.已知集合M={x|x2+x-2<0},N={x|log${\;}_{\frac{1}{2}}$x>-1},则M∩N=( )
| A. | {x|-2<x<1} | B. | {x|0<x<1} | C. | {x|x>2} | D. | ∅ |
18.函数f(x)=3x-4x3,(x∈[0,1])的最大值是( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | 0 | D. | 1 |
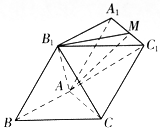 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.