题目内容
18．设M为边长为4的正方形ABCD的边BC的中点，N为正方形区域内任意一点（含边界），则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最大值为（ ）| A． | 32 | B． | 24 | C． | 20 | D． | 16 |
分析 以A为坐标原点，以AB方向为x轴正方向，以AD方向为y轴方向建立坐标系，将向量的数量积用坐标表示，再利用线性规划方法解决问题．
解答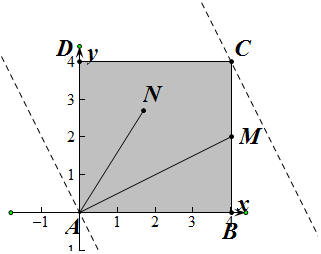 
解：以A为坐标原点，以AB方向为x轴正方向，以AD方向为y轴方向建立坐标系，
则A=（0，0），M（4，2），
则$\overrightarrow{AM}$=（4，2），
设N点坐标为（x，y），则$\overrightarrow{AN}$=（x，y），$\left\{\begin{array}{l}{0≤x≤4}\\{0≤y≤4}\end{array}\right.$，
∴$\overrightarrow{AM}$•$\overrightarrow{AN}$=4x+2y，
设z=4x+2y，平移目标函数，则过点C（4，4）时有最大值，此时最大值为z=16+8=24，
故选：B．
点评 本题主要考查两个向量的数量积公式的应用，向量的主要功能就是数形结合，将几何问题转化为代数问题，但关键是建立合适的坐标系，将向量用坐标表示，再将数量积运算转化为方程或函数问题
练习册系列答案
名校课堂系列答案
相关题目
8．已知函数f（x）=$\left\{\begin{array}{l}{kx+2，x≥0}\\{{（\frac{1}{2}）}^{x}，x＜0}\end{array}\right.$，若方程f（f（x））-$\frac{3}{2}$=0在实数集范围内无解，则实数k的取值范围是（ ）
| A． | （-1，-$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，$\frac{1}{3}$） | C． | [0，+∞） | D． | （-$\frac{1}{2}$，-$\frac{1}{4}$] |
9．在区间$[{0，\frac{π}{2}}]$上任选两个数x和y，则y＜sinx的概率为（ ）
| A． | $\frac{2}{π^2}$ | B． | $1-\frac{4}{π^2}$ | C． | $\frac{4}{π^2}$ | D． | $1-\frac{2}{π^2}$ |
10．在[0，π]内任取一个实数x，则sinx≤$\frac{1}{2}$的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
8．设函数f（x）=x2-aln（x+2），且f（x）存在两个极值点x1，x2，其中x1＜x2．
（I）求实数a的取值范围；
（II）证明不等式：$\frac{{f（{x_1}）}}{x_2}+1＜0$．
（I）求实数a的取值范围；
（II）证明不等式：$\frac{{f（{x_1}）}}{x_2}+1＜0$．
9．已知函数f（x）=$\left\{\begin{array}{l}{xln（1+x）+{x}^{2}，x≥0}\\{-xln（1-x）+{x}^{2}，x＜0}\end{array}\right.$，若f（-a）+f（a）≤2f（1），则实数a的取值范围是（ ）
| A． | （-∞，-1]∪[1，+∞） | B． | [-1，0] | C． | [0，1] | D． | [-1，1] |