题目内容
已知f(x)= 是(-∞,+∞)上的增函数,那么a的取值范围是
是(-∞,+∞)上的增函数,那么a的取值范围是
- A.[
 ,3)
,3) - B.(0,3)
- C.(1,3)
- D.(1,+∞)
A
分析:由x<1时,f(x)=(3-a)x-a是增函数解得a<3;由x≥1时,f(x)=logax是增函数,解得a>1.再由f(1)=loga1=0,(3-a)x-a=3-2a,知a .由此能求出a的取值范围.
.由此能求出a的取值范围.
解答:∵f(x)=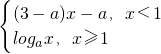 是(-∞,+∞)上的增函数,∴x<1时,f(x)=(3-a)x-a是增函数
是(-∞,+∞)上的增函数,∴x<1时,f(x)=(3-a)x-a是增函数
∴3-a>0,解得a<3;
x≥1时,f(x)=logax是增函数,解得a>1.
∵f(1)=loga1=0
∴x<1时,f(x)<0
∵x=1,(3-a)x-a=3-2a
∵x<1时,f(x)=(3-a)x-a递增
∴3-2a≤f(1)=0,解得a .
.
所以 ≤a<3.
≤a<3.
故选A.
点评:本题考查函数的单调性的应用,解题时要认真审题,仔细解答,易错点是分段函数的分界点处单调性的处理.
分析:由x<1时,f(x)=(3-a)x-a是增函数解得a<3;由x≥1时,f(x)=logax是增函数,解得a>1.再由f(1)=loga1=0,(3-a)x-a=3-2a,知a
 .由此能求出a的取值范围.
.由此能求出a的取值范围.解答:∵f(x)=
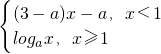 是(-∞,+∞)上的增函数,∴x<1时,f(x)=(3-a)x-a是增函数
是(-∞,+∞)上的增函数,∴x<1时,f(x)=(3-a)x-a是增函数∴3-a>0,解得a<3;
x≥1时,f(x)=logax是增函数,解得a>1.
∵f(1)=loga1=0
∴x<1时,f(x)<0
∵x=1,(3-a)x-a=3-2a
∵x<1时,f(x)=(3-a)x-a递增
∴3-2a≤f(1)=0,解得a
 .
.所以
 ≤a<3.
≤a<3.故选A.
点评:本题考查函数的单调性的应用,解题时要认真审题,仔细解答,易错点是分段函数的分界点处单调性的处理.

练习册系列答案
相关题目