题目内容
17．已知等差数列（an}，a1=5，a5=21．（1）求{an}的通项公式：
（2）求数列{an}的前n项和Sn．
分析 （1）利用公差d=$\frac{{a}_{5}-{a}_{1}}{5-1}$计算可知数列{an}是首项为5、公差为4的等差数列，进而计算可得结论；
（2）通过（1）利用等差数列的求和公式计算即得结论．
解答 解：（1）依题意，公差d=$\frac{{a}_{5}-{a}_{1}}{5-1}$=$\frac{21-5}{5-1}$=4，
∴数列{an}是首项为5、公差为4的等差数列，
故其通项公式an=5+4（n-1）=4n+1；
（2）由（1）可知Sn=$\frac{n（{a}_{1}+{a}_{n}）}{2}$=$\frac{n（5+4n+1）}{2}$=2n2+3n．
点评 本题考查数列的通项及前n项和，考查运算求解能力，注意解题方法的积累，属于基础题．
练习册系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
相关题目
5．计算sin2$\frac{π}{8}$-cos2$\frac{π}{8}$的值是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -$\frac{\sqrt{2}}{2}$ |
12．已知等比数列{an}的各项均为正数，且a1+a2=$\frac{4}{9}$，a3+a4+a5+a6=40．则$\frac{{a}_{7}+{a}_{8}+{a}_{9}}{9}$的值为117．
2．已知α∈（0，π），若cos（-α）-sin（-α）=-$\frac{1}{5}$，则tanα等于（ ）
| A． | $\frac{3}{4}$ | B． | -$\frac{3}{4}$ | C． | -$\frac{4}{3}$或-$\frac{3}{4}$ | D． | -$\frac{4}{3}$ |
6．若sin（180°+α）+cos（180°-α）=-a，则cos（540°+α）+sin（360°-α）的值是（ ）
| A． | a | B． | -a | C． | $\frac{2a}{3}$ | D． | $\frac{3a}{2}$ |
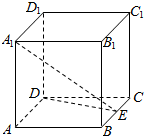如图，在正方体ABCD-A1B1C1D1中，AB=2，点E是BC的中点．