题目内容
已知数列 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 的通项公式
的通项公式 ;
;
(2)设 为数列{
为数列{ }的前n项和,求
}的前n项和,求 ;
;
(3)设 ,证明:
,证明: .
.
 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, .
.(1)求数列
 的通项公式
的通项公式 ;
;(2)设
 为数列{
为数列{ }的前n项和,求
}的前n项和,求 ;
;(3)设
 ,证明:
,证明: .
.(1) (2)
(2) (3)见解析
(3)见解析
 (2)
(2) (3)见解析
(3)见解析试题分析:
(1)当
 带入式子
带入式子 结合
结合 即可得到
即可得到 的值,当
的值,当 时,利用
时,利用 与
与 的关系(
的关系( )即可得到
)即可得到 是一个常数,即可得到数列
是一个常数,即可得到数列 为等差数列,但是需要验证
为等差数列,但是需要验证 是否符合,进而证明
是否符合,进而证明 为等差数列,即可求的通项公式.
为等差数列,即可求的通项公式.(2)把(1)中得到的
 的通项公式带入
的通项公式带入 可得
可得 ,即为等差数列与等比数列的乘积,故需要利用错位相减法来求
,即为等差数列与等比数列的乘积,故需要利用错位相减法来求 的前n项和
的前n项和 .
.(3)把(1)得到的
 带入
带入 ,观察
,观察 的通项公式为分式,为求其前n项和可以考虑利用裂项求和法.进行裂项
的通项公式为分式,为求其前n项和可以考虑利用裂项求和法.进行裂项 ,在进行求和就可以得到
,在进行求和就可以得到 的前n项和为
的前n项和为 ,利用
,利用 非负即可证明原不等式.
非负即可证明原不等式.试题解析:
(1)由题意,当
 时,有
时,有 , (1分)
, (1分)两式相减得
 即
即 . (2分)
. (2分)由
 ,得
,得 .
. 所以对一切正整数n,有
 , (3分)
, (3分)故
 ,即
,即 . (4分)
. (4分)(2)由(1),得
 ,
,所以
 ① (5分)
① (5分)①两边同乘以
 ,得
,得 ② (6分)
② (6分)①-②,得
 , (7分)
, (7分)所以
 , (8分)
, (8分)故
 . (9分)
. (9分)(3)由(1),得
 (12分)
(12分)
 (13分)
(13分) . (14分)
. (14分)
练习册系列答案
相关题目
 中,已知
中,已知 ,
, .
.  ;
; ,设数列
,设数列 的前
的前 项和为
项和为 ,试比较
,试比较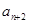 与
与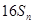 的大小.
的大小. 中,已知
中,已知 .
. 项和
项和 .
. ,求
,求 的前
的前 .
. 中,
中, ,
, (
( ),则该数列的前2014项的和是.
),则该数列的前2014项的和是.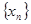 :
: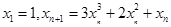 ;数列
;数列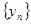 :
: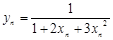 ;数列
;数列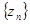 :
: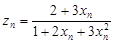 ;若
;若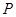 ,
,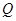 ,那么
,那么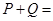 ( )
( )
 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于
等于



 ,则S4=________.
,则S4=________. ,且
,且 ,则
,则 ( )
( )