题目内容
cos（α-35°）cos（25°+α）+sin（α-35°）sin（25°+α）的值为（ ）
分析：根据两角和的余弦公式，原式等于cos[（α-35°）-（α+25°）]=cos60°，再根据特殊角的三角函数值即可算出所求式子的值．
解答：解：根据题意，可得
cos（α-35°）cos（25°+α）+sin（α-35°）sin（25°+α）
=cos[（α-35°）-（α+25°）]=cos（-60°）=cos60°=
．
故选：B
cos（α-35°）cos（25°+α）+sin（α-35°）sin（25°+α）
=cos[（α-35°）-（α+25°）]=cos（-60°）=cos60°=
| 1 |
| 2 |
故选：B
点评：本题求一个三角函数式子的值，着重考查了诱导公式、特殊角的三角函数值与两角和的余弦公式等知识，属于基础题．
练习册系列答案
考前必练系列答案
相关题目
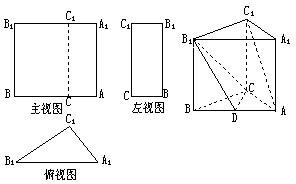已知三棱柱ABC-A1B1C1的三视图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，
如图所示，角a的终边与单位圆（圆心在原点，半径为1的圆）交于第二象限的点A（cosα，