题目内容
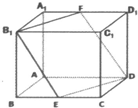 已知棱长为a的正方体ABCD-A1B1C1D1,E、F分别是BC,A1D1的中点.
已知棱长为a的正方体ABCD-A1B1C1D1,E、F分别是BC,A1D1的中点.(1)求证:四边形B1EDF是菱形;
(2)求AD与面B1EDF所成的角.
分析:(1)要证四边形B1EDF为菱形,只要先证其是平行四边形,再说明邻边相等即可,根据正方体的性质易证;
(2)证明直线AD与平面B1EDF所成的角为∠ADB1,在直角△B1AD中,利用余弦定理,即可求得直线AD与平面B1EDF所成的角;
(2)证明直线AD与平面B1EDF所成的角为∠ADB1,在直角△B1AD中,利用余弦定理,即可求得直线AD与平面B1EDF所成的角;
解答: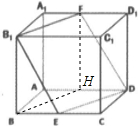 证明:(1)取AD中点H,连接BH,FH,
证明:(1)取AD中点H,连接BH,FH,
易证:FHBB1为矩形,
因此,FB1∥BH,且FB1=BH,.
又∵正方形ABCD中BH∥DE且BH=DE,
∴FB1∥DE,FB1=DE,
∴FB1ED为平行四边形.
又∵FD=DE=
a,
∴四边形B1EDF为菱形.
解:(2)∵平面ADE⊥平面ADF
∴AD在平面B1EDF内的射影在∠EDF的平分线上,而四边形B1EDF是菱形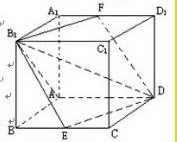
∴DB1为∠EDF的平分线
∴直线AD与平面B1EDF所成的角为∠ADB1.
在直角△B1AD中,AD=a,AB1=
a,B1D=
a,
∴cos∠ADB1=
=
∴直线AD与平面B1EDF所成的角为arccos
;
 证明:(1)取AD中点H,连接BH,FH,
证明:(1)取AD中点H,连接BH,FH,易证:FHBB1为矩形,
因此,FB1∥BH,且FB1=BH,.
又∵正方形ABCD中BH∥DE且BH=DE,
∴FB1∥DE,FB1=DE,
∴FB1ED为平行四边形.
又∵FD=DE=
| ||
| 2 |
∴四边形B1EDF为菱形.
解:(2)∵平面ADE⊥平面ADF
∴AD在平面B1EDF内的射影在∠EDF的平分线上,而四边形B1EDF是菱形

∴DB1为∠EDF的平分线
∴直线AD与平面B1EDF所成的角为∠ADB1.
在直角△B1AD中,AD=a,AB1=
| 2 |
| 3 |
∴cos∠ADB1=
| a2+3a2-2a2 | ||
2×a×
|
| ||
| 3 |
∴直线AD与平面B1EDF所成的角为arccos
| ||
| 3 |
点评:此题是个中档题.考查的知识点是直线与平面所成的角,其中求出直线AD与平面B1EDF所成的角为∠ADB1是解答的关键.

练习册系列答案
相关题目

 已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.
已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.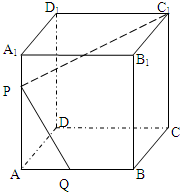 (理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.
(理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.