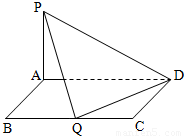
题目内容
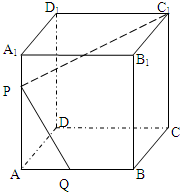 (理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.
(理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.(I)在AB上找出一点Q,使C1P⊥PQ;
(II)求当C1P⊥PQ时,线段AQ的长.
分析:(I)直接设出A1P=x,AP=1-x,AQ=y;根据直角三角形求出RT△C1PQ三边长,结合勾股定理即可求出点Q所满足的条件;
(II)直接由第一问的结论即可得到线段AQ的长.
(II)直接由第一问的结论即可得到线段AQ的长.
解答:解:(I)设A1P=x,AP=1-x,AQ=y.
∴
=
⇒x=
,AP=
∴C1P=
=
=
;
PQ=
=
;
C1Q=
=
=
;
因为C1P⊥PQ,
∴C 1P2+PQ 2=C 1Q2⇒2+(
)2+(
) 2+y2=2+(1-y)2⇒y=
;
∴当AQ=
时C1P⊥PQ;
(II)由第一问得:AQ=
.
∴
| x |
| 1-x |
| m |
| n |
| m |
| m+n |
| n |
| m+n |
∴C1P=
| A1C12+A1P2 |
(
|
2+(
|
PQ=
| AP 2+AQ2 |
(
|
C1Q=
| CC 12+CQ 2 |
| CC 12+CB 2+BQ 2 |
| 12+12+(1-y) 2 |
因为C1P⊥PQ,
∴C 1P2+PQ 2=C 1Q2⇒2+(
| m |
| m+n |
| n |
| m+n |
| mn |
| (m+n) 2 |
∴当AQ=
| mn |
| (m+n) 2 |
(II)由第一问得:AQ=
| mn |
| (m+n) 2 |
点评:本题是中档题,考查直角三角形的利用以及长方体的性质,考查计算能力.解决本题的关键在于利用勾股定理求出AQ的长.

练习册系列答案
相关题目
 如图,已知椭圆
如图,已知椭圆 (理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:
(理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题: