题目内容
 已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.
已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD,AD的中点.(1)求证:四边形MNA1C1是梯形;
(2)求证:∠DNM=∠D1A1C1.
分析:(1)欲证四边形MN A1C1是梯形,只须证其一组对边平行且不等即可,连接AC,在△ACD中,M,N分别是棱CD,AD的中点,根据三角形的中位线定理即可证得;
(2)根据平行公理可知MN∥A1C1,又∵ND∥A1D1,从而有∠DNM与∠D1A1C1相等或互补,而∠DNM与∠D1A1C1均是直角三角形的锐角,故可证出∠DNM=∠D1A1C1
(2)根据平行公理可知MN∥A1C1,又∵ND∥A1D1,从而有∠DNM与∠D1A1C1相等或互补,而∠DNM与∠D1A1C1均是直角三角形的锐角,故可证出∠DNM=∠D1A1C1
解答:证明:(1)连接AC,在△ACD中,
∵M,N分别是棱CD,AD的中点,
∴MN是三角形的中位线,
∴MN∥AC,MN=
AC.由正方体的性质得:AC∥A1C1,AC=A1C1.
∴MN∥A1C1,且MN=
A1C1,即MN≠A1C1,
∴四边形MN A1C1是梯形.
(2)由(1)可知MN∥A1C1,又∵ND∥A1D1,
∴∠DNM与∠D1A1C1相等或互补,而∠DNM与∠D1A1C1均是直角三角形的锐角,
∴∠DNM=∠D1A1C1
∵M,N分别是棱CD,AD的中点,
∴MN是三角形的中位线,
∴MN∥AC,MN=
| 1 |
| 2 |
∴MN∥A1C1,且MN=
| 1 |
| 2 |
∴四边形MN A1C1是梯形.
(2)由(1)可知MN∥A1C1,又∵ND∥A1D1,
∴∠DNM与∠D1A1C1相等或互补,而∠DNM与∠D1A1C1均是直角三角形的锐角,
∴∠DNM=∠D1A1C1
点评:本小题主要考查棱柱的结构特征、空间位置关系等基础知识,考查运算求解能力,考查空间想象能力.属于基础题.

练习册系列答案
相关题目

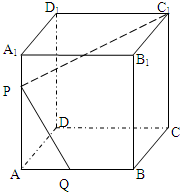 (理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.
(理科做)如图,已知棱长为a的正方体ABCD-A1B1C1D1中,P是棱AA1上的一点,且A1P:PA=m:n.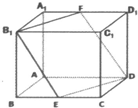 已知棱长为a的正方体ABCD-A1B1C1D1,E、F分别是BC,A1D1的中点.
已知棱长为a的正方体ABCD-A1B1C1D1,E、F分别是BC,A1D1的中点.