题目内容
过点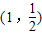 作圆x2+y2=1的切线,切点分别为A,B.若直线AB恰好经过椭圆
作圆x2+y2=1的切线,切点分别为A,B.若直线AB恰好经过椭圆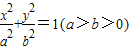 的焦点和上顶点,则椭圆方程为 .
的焦点和上顶点,则椭圆方程为 .
【答案】分析:方法一:利用圆的方程相减即可得出两圆相交的交点所在的直线的方程,进而得出椭圆的焦点、顶点,再利用椭圆的性质即可得出方程.
方法二:易知直线x=1是圆的一条切线,即可得出切点为A(1,0);设另一条切线的斜率为k,则切线方程为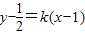 ,利用切线的性质和点到直线的距离公式可得圆心(0,0)到切线的距离d=r,可得斜率k,进而得到切线方程和切点.
,利用切线的性质和点到直线的距离公式可得圆心(0,0)到切线的距离d=r,可得斜率k,进而得到切线方程和切点.
解答:解:方法一:设点P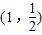 ,O(0,0).则以线段OP为直径的圆的方程为:
,O(0,0).则以线段OP为直径的圆的方程为: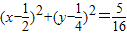 .与方程x2+y2=1相减得
.与方程x2+y2=1相减得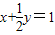 .
.
令x=0,得y=2;令y=0,得x=1.
∴焦点为(1,0),上顶点为(0,2).
∴c=1,b=2.a2=b2+c2=5.
∴椭圆的方程为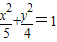 .
.
方法二:易知直线x=1是圆的一条切线,切点为A(1,0);
设另一条切线的斜率为k,则切线方程为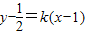 ,化为2kx-2y+1-2k=0,则
,化为2kx-2y+1-2k=0,则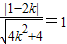 ,解得
,解得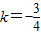 ,得切线方程为3x+4y-5=0.
,得切线方程为3x+4y-5=0.
联立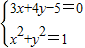 解得切点B
解得切点B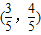 .
.
∴直线AB的方程为:2x+y-2=0.以下同方法一.
点评:熟练掌握椭圆的标准方程及其性质、两圆的根轴方程的求法、直线与圆相切的性质、点到直线的距离公式等是解题的关键.
方法二:易知直线x=1是圆的一条切线,即可得出切点为A(1,0);设另一条切线的斜率为k,则切线方程为
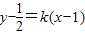 ,利用切线的性质和点到直线的距离公式可得圆心(0,0)到切线的距离d=r,可得斜率k,进而得到切线方程和切点.
,利用切线的性质和点到直线的距离公式可得圆心(0,0)到切线的距离d=r,可得斜率k,进而得到切线方程和切点.解答:解:方法一:设点P
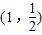 ,O(0,0).则以线段OP为直径的圆的方程为:
,O(0,0).则以线段OP为直径的圆的方程为: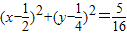 .与方程x2+y2=1相减得
.与方程x2+y2=1相减得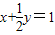 .
.令x=0,得y=2;令y=0,得x=1.
∴焦点为(1,0),上顶点为(0,2).
∴c=1,b=2.a2=b2+c2=5.
∴椭圆的方程为
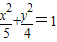 .
.方法二:易知直线x=1是圆的一条切线,切点为A(1,0);
设另一条切线的斜率为k,则切线方程为
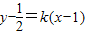 ,化为2kx-2y+1-2k=0,则
,化为2kx-2y+1-2k=0,则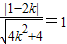 ,解得
,解得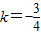 ,得切线方程为3x+4y-5=0.
,得切线方程为3x+4y-5=0.联立
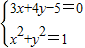 解得切点B
解得切点B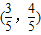 .
.∴直线AB的方程为:2x+y-2=0.以下同方法一.
点评:熟练掌握椭圆的标准方程及其性质、两圆的根轴方程的求法、直线与圆相切的性质、点到直线的距离公式等是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 (2012•长春模拟)已知椭圆
(2012•长春模拟)已知椭圆 的焦距为2c,过点
的焦距为2c,过点 作圆x2+y2=a2的两条切线,切点分别为M,N.若椭圆的离心率的取值范围为
作圆x2+y2=a2的两条切线,切点分别为M,N.若椭圆的离心率的取值范围为 ,则∠MPN的取值范围为( )
,则∠MPN的取值范围为( )



 作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆的面积为 .
作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆的面积为 .