题目内容
设 为奇函数,则使
为奇函数,则使 的实数
的实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
D
解析试题分析:函数的定义域为 即
即 ,因为函数为奇函数,所以定义域关于原点对称,所以当x=-1时,ax-(a+2)=0,解得a=-1,函数的定义域为
,因为函数为奇函数,所以定义域关于原点对称,所以当x=-1时,ax-(a+2)=0,解得a=-1,函数的定义域为 ,所以函数
,所以函数 ,不等式
,不等式 可转化为
可转化为 ,解得
,解得 或
或 ,与定义域取交集得
,与定义域取交集得 ,答案选D.
,答案选D.
考点:函数的性质与应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 的定义域为
的定义域为 ,则
,则 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
设偶函数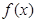 的定义域为
的定义域为 ,
,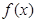 在区间
在区间 上为增函数,则
上为增函数,则 的
的
大小关系是( )
A. | B. |
C. | D. |
下列各组函数是同一函数的是( )
① 与
与 ;
;
② 与
与 ;
;
③ 与
与 ;
;
④ 与
与 。
。
| A.①② | B.①③ | C.③④ | D.①④ |
定义运算 为:
为: 如
如 ,则函数
,则函数 的值域为
的值域为
| A.R | B.(0,1] | C.(0,+∞) | D.[1,+∞) |
设偶函数 对任意
对任意 都有
都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
| A.10 | B. | C.-10 | D. |
已知 是R上的单调递增函数,则实数a的取值范围为( )
是R上的单调递增函数,则实数a的取值范围为( )
| A.(1,+∞) | B.(1,8) | C.(4,8) | D.[4,8) |
 ”的否命题为“若
”的否命题为“若 ”;
”; 则
则 ”的逆命题为真命题;
”的逆命题为真命题; ”的否定是“
”的否定是“ ”;
”;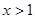 ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件. 的图象是( )
的图象是( )