题目内容
已知 是R上的单调递增函数,则实数a的取值范围为( )
是R上的单调递增函数,则实数a的取值范围为( )
| A.(1,+∞) | B.(1,8) | C.(4,8) | D.[4,8) |
D
解析试题分析:∵当x≤1时, 为增函数∴
为增函数∴ ,又∵当x>1时,
,又∵当x>1时, 为增函数∴a>1同时,当x=1时,函数对应于一次函数的取值要小于指数函数的取值∴
为增函数∴a>1同时,当x=1时,函数对应于一次函数的取值要小于指数函数的取值∴ ,综上所述,4≤a<8,故选B.
,综上所述,4≤a<8,故选B.
考点:函数单调性的判断与证明.

练习册系列答案
相关题目
设 为奇函数,则使
为奇函数,则使 的实数
的实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
函数 在
在 上为减函数,则实数
上为减函数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
已知函数 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 ,其中
,其中 ,对应法则
,对应法则 ,对应实数
,对应实数 ,在集合
,在集合 中不存在原像,则
中不存在原像,则 取值范围是( )
取值范围是( )
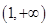
 的最小值是 .
的最小值是 . =
= ,则
,则 = .
= . 上的奇函数,且
上的奇函数,且 的图象关于直线
的图象关于直线 对称,则
对称,则 .
.