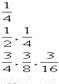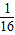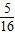题目内容
如图给出了一个“等差数阵”:其中每行、每列都是等差数列,aij表示位于第i行第j列的数.
(Ⅰ)写出a45的值;
(Ⅱ)写出aij的计算公式.

(Ⅰ)写出a45的值;
(Ⅱ)写出aij的计算公式.

分析:(I)由等差数列先求出第一列第四项,再由等差数列求第四行第五项;
(II)由(I)寻求规律,第一列的第i项,作为第i行的首项,公差为2i+1,进而由等差数列的通项公式求得aij.
(II)由(I)寻求规律,第一列的第i项,作为第i行的首项,公差为2i+1,进而由等差数列的通项公式求得aij.
解答:解:(II)该等差数阵的第1列是首项为4,公差为3的等差数列,
a41=4+3×(4-1)=13,第2列是首项为7,公差为5的等差数列,
a42=7+5×(4-1)=22.∵a41=13,a42=22,
∴第4行是首项为13,公差为9的等差数列.
∴a45=13+9×(5-1)=49.(6分)
(II)∵a1j=4+3(j-1),a2j=7+5(j-1),
∴第j列是首项为4+3(j-1),公差为2j+1的等差数列.
∴aij=4+3(j-1)+(2j+1)•(i-1)=i(2j+1)+j.(12分)
a41=4+3×(4-1)=13,第2列是首项为7,公差为5的等差数列,
a42=7+5×(4-1)=22.∵a41=13,a42=22,
∴第4行是首项为13,公差为9的等差数列.
∴a45=13+9×(5-1)=49.(6分)
(II)∵a1j=4+3(j-1),a2j=7+5(j-1),
∴第j列是首项为4+3(j-1),公差为2j+1的等差数列.
∴aij=4+3(j-1)+(2j+1)•(i-1)=i(2j+1)+j.(12分)
点评:本小题主要考查等差数列等基本知识,考查逻辑思维能力、分析问题和解决问题的能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
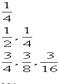 如图给出了一个“三角形数阵”.已知每一列数成等差数列,从第三行起,每一行数成等比数列,而且每一行的公比都相等,记第i行第j列的数为aij(i、j∈N*),则a53的值为( )
如图给出了一个“三角形数阵”.已知每一列数成等差数列,从第三行起,每一行数成等比数列,而且每一行的公比都相等,记第i行第j列的数为aij(i、j∈N*),则a53的值为( )