题目内容
(坐标系与参数方程选做题)已知直线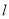 的方程是
的方程是 (
(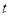 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,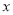 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆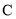 的极坐标方程为
的极坐标方程为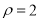 ,则圆
,则圆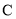 上的点到直线
上的点到直线 的距离的最小值是 .
的距离的最小值是 .

【解析】
试题分析:把直线l的参数方程 化为普通为成为x-y+4=0,把圆C的极坐标方程
化为普通为成为x-y+4=0,把圆C的极坐标方程 化为普通方程为
化为普通方程为 ,圆心坐标为(0,0),半径为2,圆心到直线l的距离为
,圆心坐标为(0,0),半径为2,圆心到直线l的距离为 ,∴圆C上的点到直线l的距离的最小值为
,∴圆C上的点到直线l的距离的最小值为 .
.
考点:考查了参数方程,极坐标方程和普通方程的互化,掌握圆心到直线的距离减去半径即为圆上的点到直线距离的最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
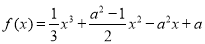 ,
,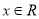 ,
,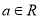 .
.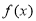 在区间
在区间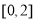 内恰有两个零点,求实数
内恰有两个零点,求实数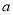 的取值范围;
的取值范围;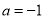 ,设函数
,设函数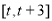 上的最大值为
上的最大值为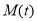 ,最小值为
,最小值为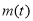 ,记
,记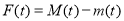 ,求函数
,求函数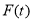 在区间
在区间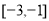 上的最小值.
上的最小值. ,
, ,下列结论成立的是( )
,下列结论成立的是( ) B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 ,都有
,都有 ,记
,记 .
. ,
, 的值;
的值; 的通项公式;
的通项公式; ,数列
,数列 的前
的前 项和为
项和为 ,证明:对于任意的
,证明:对于任意的 ,都有
,都有 .
. 的解集是____________.
的解集是____________. 的四个函数
的四个函数 ,
, ,
, ,
, 中,奇函数的个数是( )
中,奇函数的个数是( ) B.
B. C.
C. D.
D.
 的值域是( )
的值域是( ) C.
C. D.
D.
 ,下列命题中正确的是( )
,下列命题中正确的是( ) ,
, ,则a‖b
,则a‖b  ,则a‖b
,则a‖b