题目内容
(本小题满分14分)若数列 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 ,都有
,都有
 ,记
,记 .
.
(1)求 ,
, 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)令 ,数列
,数列 的前
的前 项和为
项和为 ,证明:对于任意的
,证明:对于任意的 ,都有
,都有 .
.
(1) ;(2)
;(2) ;(3)见解析
;(3)见解析
【解析】
试题分析:(1)【解析】
由 得:
得:
解得 1分
1分
由 得:
得:
解得 3分
3分
(2)【解析】
由 ①
①
当 时,有
时,有 ② 4分
② 4分
①-②得: 5分
5分
∴数列 是首项
是首项 ,公比
,公比 的等比数列 6分
的等比数列 6分
∴ 7分
7分
∴ 8分
8分
(3)证明:由(2)有 10分
10分
 12分
12分 13分
13分
 14分
14分
考点:考查了等比数列和裂项相消法求和,数列与不等式的综合.

练习册系列答案
相关题目
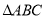 的重心为G,角A,B,C所对的边分别为
的重心为G,角A,B,C所对的边分别为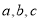 ,若
,若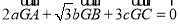 ,则
,则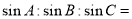
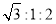 C.
C.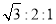 D.
D.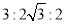
 的右焦点
的右焦点 作垂直于
作垂直于 轴的直线,交双曲线的渐近线于
轴的直线,交双曲线的渐近线于 两点,若
两点,若 (
( 为坐标原点)是等边三角形,则双曲线的离心率为 ( )
为坐标原点)是等边三角形,则双曲线的离心率为 ( ) B.
B. C.
C. D.
D.
 ,
, ,定义
,定义 ,其中
,其中 是
是 的共轭复数.对任意复数
的共轭复数.对任意复数 ,
, ,
, ,有如下四个命题:
,有如下四个命题: ;
; ;
; ;
; .
. B.
B. C.
C. D.
D.
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
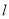 的方程是
的方程是 (
(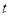 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,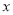 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆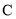 的极坐标方程为
的极坐标方程为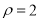 ,则圆
,则圆 上的点到直线
上的点到直线 的距离的最小值是 .
的距离的最小值是 . 是
是 上的单调函数,则实数
上的单调函数,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 为奇函数,且在
为奇函数,且在 上是减函数,又
上是减函数,又  ,则
,则 的解集为( )
的解集为( )


 的距离是 .
的距离是 .