题目内容
已知椭圆C:
+
=1(a>b>0)的焦距为2
,长轴长是短轴长的2倍.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)斜率为k的直线l交椭圆于A、B两点,其中A点为椭圆的左顶点,若椭圆的上顶点P始终在以AB为直径的圆内,求实数k的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)斜率为k的直线l交椭圆于A、B两点,其中A点为椭圆的左顶点,若椭圆的上顶点P始终在以AB为直径的圆内,求实数k的取值范围.
考点:椭圆的简单性质
专题:综合题,方程思想,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据椭圆的几何性质,列出方程组
,求出a、b的值即可;
(Ⅱ)写出直线l的方程,与椭圆方程联立,求出点B的坐标,利用P在以AB为直径的圆内,
•
<0,求出k的取值范围.
|
(Ⅱ)写出直线l的方程,与椭圆方程联立,求出点B的坐标,利用P在以AB为直径的圆内,
| PA |
| PB |
解答:
解:(Ⅰ)根据题意,得
;
解得a=2,b=1;
∴椭圆的标准方程为
+y2=1;
(Ⅱ)由(Ⅰ)及题意,知顶点A为(-2,0),
∴直线l的方程为y=k(x+2),
与椭圆方程联立,得
;
消去y,得(1+4k2)x2+16k2x+(16k2-4)=0;
设点B为(x0,y0),则x0-2=-
,
∴x0=
,y0=
;
又椭圆的上顶点P在以AB为直径的圆内,
∴∠APB为钝角,即
•
<0;
∵P(0,1),A(-2,0),B(
,
),
∴
=(-2,-1),
=(
,
);
∴
+
<0,
即20k2-4k-3<0,解得k∈(-
,
).
|
解得a=2,b=1;
∴椭圆的标准方程为
| x2 |
| 4 |
(Ⅱ)由(Ⅰ)及题意,知顶点A为(-2,0),
∴直线l的方程为y=k(x+2),
与椭圆方程联立,得
|
消去y,得(1+4k2)x2+16k2x+(16k2-4)=0;
设点B为(x0,y0),则x0-2=-
| 16k2 |
| 1+4k2 |
∴x0=
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
又椭圆的上顶点P在以AB为直径的圆内,
∴∠APB为钝角,即
| PA |
| PB |
∵P(0,1),A(-2,0),B(
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
∴
| PA |
| PB |
| 2-8k2 |
| 1+4k2 |
| -4k2+4k-1 |
| 1+4k2 |
∴
| 16k2-4 |
| 1+4k2 |
| 4k2-4k+1 |
| 1+4k2 |
即20k2-4k-3<0,解得k∈(-
| 3 |
| 10 |
| 1 |
| 2 |
点评:本题考查了椭圆的几何性质的应用问题,也考查了直线与椭圆方程的综合应用问题,考查了方程思想的应用,是综合性题目.

练习册系列答案
相关题目
函数f(x)=sinxsin(
+x)-x的零点的个数为( )
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
已知△ABC的三边长分别为a、b、c,且满足b+c≤3a,则
的取值范围是( )
| c |
| a |
| A、(1,+∞) |
| B、(0,2) |
| C、(1,3) |
| D、(0,3) |
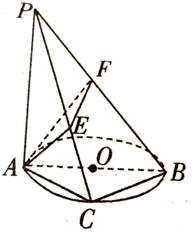 如图,AB是圆O的直径,C为圆周上一点,PA⊥平面ABC,若AE⊥PC,F是PD上任意一点,求证:平面AEF⊥平面PBC.
如图,AB是圆O的直径,C为圆周上一点,PA⊥平面ABC,若AE⊥PC,F是PD上任意一点,求证:平面AEF⊥平面PBC.