题目内容
如图所示,在三棱锥P—ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,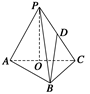
OP⊥底面ABC.
(1)若k=1,试求异面直线PA与BD所成角余弦值的大小;
(2)当k取何值时,二面角O—PC—B的大小为 ?
?

OP⊥底面ABC.
(1)若k=1,试求异面直线PA与BD所成角余弦值的大小;
(2)当k取何值时,二面角O—PC—B的大小为
 ?
?(1) 异面直线PA与BD所成角的余弦值的大小为 . (2)k=
. (2)k= 时,二面角O—PC—B的大小为
时,二面角O—PC—B的大小为
 . (2)k=
. (2)k= 时,二面角O—PC—B的大小为
时,二面角O—PC—B的大小为
∵OP⊥平面ABC,又OA=OC,AB=BC,

从而OA⊥OB,OB⊥OP,OA⊥OP,
以O为原点,建立如图所示空间直角坐标系O—xyz.
(1)设AB=a,则PA=a,PO= a,
a,
A( a,0,0),B(0,
a,0,0),B(0, a,0),
a,0),
C(- a,0,0),P(0,0,
a,0,0),P(0,0, a),
a),
则D(- a,0,
a,0, a).
a).
∵ =(
=( a,0,-
a,0,- a ),
a ), =(-
=(- a,-
a,- a,
a, a),
a),
∴cos〈 ,
, 〉=
〉= =
= =-
=- ,
,
则异面直线PA与BD所成角的余弦值的大小为 .
.
(2)设AB=a,OP=h,∵OB⊥平面POC,
∴ =(0,
=(0, a,0)为平面POC的一个法向量.
a,0)为平面POC的一个法向量.
不妨设平面PBC的一个法向量为n=(x,y,z),
∵A( a,0,0),B(0,
a,0,0),B(0, a,0),C(-
a,0),C(- a,0,0),P(0,0,h),
a,0,0),P(0,0,h),
∴ =(-
=(- a,-
a,-  a,0),
a,0), ="(-"
="(-"  a,0,-h),
a,0,-h),
由


不妨令x=1,则y=-1,z=- ,
,
即n="(1,-1,-" ),则cos
),则cos =
=
= =
=
 2+
2+ =4
=4 h=
h= a,
a,
∴PA= =
= =
= a,
a,
而AB=kPA,∴k= .
.
故当k= 时,二面角O—PC—B的大小为
时,二面角O—PC—B的大小为 .
.

从而OA⊥OB,OB⊥OP,OA⊥OP,
以O为原点,建立如图所示空间直角坐标系O—xyz.
(1)设AB=a,则PA=a,PO=
 a,
a,A(
 a,0,0),B(0,
a,0,0),B(0, a,0),
a,0),C(-
 a,0,0),P(0,0,
a,0,0),P(0,0, a),
a),则D(-
 a,0,
a,0, a).
a).∵
 =(
=( a,0,-
a,0,- a ),
a ), =(-
=(- a,-
a,- a,
a, a),
a),∴cos〈
 ,
, 〉=
〉= =
= =-
=- ,
,则异面直线PA与BD所成角的余弦值的大小为
 .
.(2)设AB=a,OP=h,∵OB⊥平面POC,
∴
 =(0,
=(0, a,0)为平面POC的一个法向量.
a,0)为平面POC的一个法向量.不妨设平面PBC的一个法向量为n=(x,y,z),
∵A(
 a,0,0),B(0,
a,0,0),B(0, a,0),C(-
a,0),C(- a,0,0),P(0,0,h),
a,0,0),P(0,0,h),∴
 =(-
=(- a,-
a,-  a,0),
a,0), ="(-"
="(-"  a,0,-h),
a,0,-h),由



不妨令x=1,则y=-1,z=-
 ,
,即n="(1,-1,-"
 ),则cos
),则cos =
=
=
 =
=
 2+
2+ =4
=4 h=
h= a,
a,∴PA=
 =
= =
= a,
a,而AB=kPA,∴k=
 .
.故当k=
 时,二面角O—PC—B的大小为
时,二面角O—PC—B的大小为 .
.
练习册系列答案
相关题目
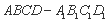 中,
中,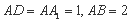 .
. 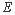 在对角线
在对角线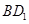 上移动,求证:
上移动,求证: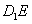 ⊥
⊥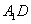 ;
; 中点时,求点
中点时,求点 的距离。
的距离。 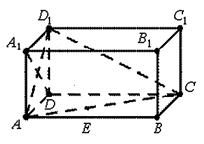
 并确定
并确定 的关系,使
的关系,使 轴垂直.
轴垂直. 中,
中, 是正三角形,
是正三角形, ,D是
,D是 的中点,二面角
的中点,二面角 为120,
为120, ,
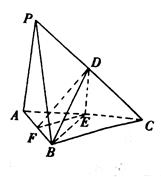
, .取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
.取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,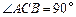 ,侧棱
,侧棱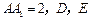 分别是
分别是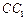 与
与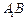 的中点,点
的中点,点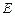 在平面
在平面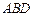 上的射影是
上的射影是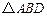 的重心
的重心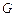 ,求点
,求点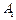 到平面
到平面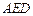 的距离.
的距离.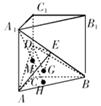
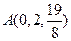 ,
,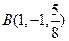 ,
,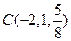 是平面
是平面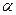 内的三点,设平面
内的三点,设平面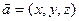 ,则
,则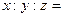 ________________。
________________。