题目内容
平面上两点A(-1,0)、B(1,0),在圆C:(x-3)2+(y-4)2=4上取一点P,求使|AP|2+|BP|2取得最小值时点P的坐标.
解法一:∵点P在圆C:(x-3)2+(y-4)2=4上,
∴可设P点的坐标为(3+2cosθ,4+2sinθ).
又A(-1,0)、B(1,0),
∴|AP|2+|BP|2=(3+2cosθ+1)2+(4+2sinθ)2+(3+2cosθ-1)2+(4+2sinθ)2=60+32sinθ+24cosθ=60+40sin(θ+![]() )(其中tan
)(其中tan![]() =
=![]() ).
).
当sin(θ+![]() )=-1时,(|AP|2+|BP|2)min=20,
)=-1时,(|AP|2+|BP|2)min=20,
此时60+24cosθ+32sinθ=20,即3cosθ+4sinθ=-5.
由![]() 得
得
∴P点的坐标为(![]() ,
,![]() ).
).
解法二:设P点的坐标为(x,y).
∵A(-1,0)、B(1,0),
∴|AP|2+|BP|2=(x+1)2+y2+(x-1)2+y2=2(x2+y2)+2=2|OP|2+2.
要使|AP|2+|BP|2取得最小值,需使|OP|2最小.
又点P为圆C:(x-3)2+(y-4)2=4上的点,∴(|OP|)min=|OC|-r(r为半径).
由(x-3)2+(y-4)2=4,知C(3,4),r=2.
∴|OC|-r=![]() -2=5-2=3,即(|OP|)min=3.
-2=5-2=3,即(|OP|)min=3.
∴(|AP|2+|BP|2)min=2×32+2=20.此时,OC:y=![]() x.
x.
由 得
得 或
或 (舍).
(舍).
∴点P的坐标为(![]() ,
,![]() ).
).
点评:解法一是利用了圆的参数方程的形式设出了点P的坐标,使所求的式子转化为三角函数式,利用三角函数法求最值;解法二设出的是P点的普通坐标(x,y),使要求的式子转化为求圆上的点到原点的距离问题,利用数形结合法求最值.

练习册系列答案
相关题目
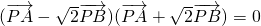 .
.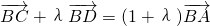 ,求的取值范围.
,求的取值范围.