题目内容
已知平面上两点A(-1,0),B(0,0),P为该平面上一动点,若(
-
)•(
+
)=0.
(1)问点P在什么曲线上?并求出该曲线方程.
(2)若C、D两点在点P的轨迹上,若
+λ
=(1+λ)
,求的取值范围.
| PA |
| 2 |
| PB |
| PA |
| 2 |
| PB |
(1)问点P在什么曲线上?并求出该曲线方程.
(2)若C、D两点在点P的轨迹上,若
| BC |
| BD |
| BA |
分析:(1)用坐标表示向量,利用向量的数量积运算,化简整理可得曲线及方程;
(2)利用
+λ
=(1+λ)
,确定坐标之间的关系,再结合圆的方程门禁卡求得结论.
(2)利用
| BC |
| BD |
| BA |
解答:解:(1)设P(x,y),∵A(-1,0),B(0,0),
∴
=(-1-x,-y),
=(-1-x,-y)
由(
-
)•(
+
)=0得,
2=2
2,即(x+1)2+y2=2x2+2y2,
化简整理得(x-1)2+y2=2,
∴点P在以(1,0)为圆心,
为半径的圆上,方程为(x-1)2+y2=2.------------------------(4分)
(2)设C(x1,y1),D(x2,y2)
∵
+λ
=(1+λ)
,
∴
,∴
①,
∵点C(x1,y1)在圆上,∴(x1-1)2+y12=2②,
将①代入②得,[λ(x2-1)+,
化简整理得(λ+1)(2λx2+λ+1)=0,即λ=-1或2λx2+λ+1=0.
由2λx2+λ+1=0得x2=-
,
又∵1-
≤x2≤1+
,∴1-
≤-
≤1+
,
∴-2
-3≤λ≤2
-3.-----------------------(12分)
∴
| PA |
| PB |
由(
| PA |
| 2 |
| PB |
| PA |
| 2 |
| PB |
| PA |
| PB |
化简整理得(x-1)2+y2=2,
∴点P在以(1,0)为圆心,
| 2 |
(2)设C(x1,y1),D(x2,y2)
∵
| BC |
| BD |
| BA |
∴
|
|
∵点C(x1,y1)在圆上,∴(x1-1)2+y12=2②,
将①代入②得,[λ(x2-1)+,
化简整理得(λ+1)(2λx2+λ+1)=0,即λ=-1或2λx2+λ+1=0.
由2λx2+λ+1=0得x2=-
| 1+λ |
| 2λ |
又∵1-
| 2 |
| 2 |
| 2 |
| 1+λ |
| 2λ |
| 2 |
∴-2
| 2 |
| 2 |
点评:本题考查轨迹方程,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 最大,求M的坐标及最大值
最大,求M的坐标及最大值
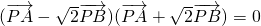 .
.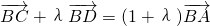 ,求的取值范围.
,求的取值范围.