题目内容
设向量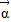 =(
=(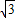 sin2x,sinx+cosx),
sin2x,sinx+cosx),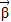 =(1,sinx-cosx),其中x∈R,函数f(x)=
=(1,sinx-cosx),其中x∈R,函数f(x)=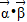 .(1)求f(x) 的最小正周期;
.(1)求f(x) 的最小正周期;(2)若f(θ)=
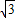 ,其中0<θ<
,其中0<θ<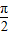 ,求cos(θ+
,求cos(θ+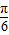 )的值.
)的值.
【答案】分析:(1)利用向量的数量积、倍角公式、两角和差的正弦余弦公式、周期公式即可得出;
(2)利用(1)的结论即可得出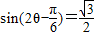 .再利用正弦函数的单调性和θ的取值范围、两角和的余弦公式即可得出.
.再利用正弦函数的单调性和θ的取值范围、两角和的余弦公式即可得出.
解答:解:(1)∵f(x)=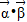 =
=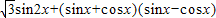
=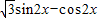
=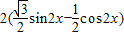
=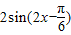 ,
,
∴T=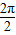 =π.即f (x) 的最小正周期为π.
=π.即f (x) 的最小正周期为π.
(2)∵f (θ)=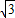 ,∴
,∴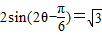 ,∴
,∴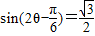 .
.
∵0<θ<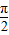 ,∴
,∴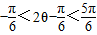 ,∴
,∴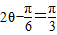 或
或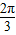 .
.
解得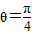 或
或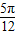 .
.
∴当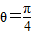 时,
时,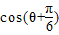 =
=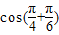 =
=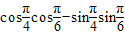 =
=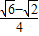 ;
;
当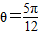 时,
时,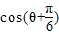 =
=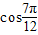 =-
=-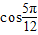 =
=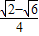 .
.
点评:熟练掌握三角函数的单调性、倍角公式、两角和差的正弦余弦公式、周期公式、向量的数量积是解题的关键.
(2)利用(1)的结论即可得出
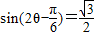 .再利用正弦函数的单调性和θ的取值范围、两角和的余弦公式即可得出.
.再利用正弦函数的单调性和θ的取值范围、两角和的余弦公式即可得出.解答:解:(1)∵f(x)=
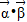 =
=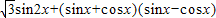
=
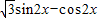
=
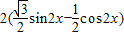
=
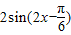 ,
,∴T=
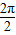 =π.即f (x) 的最小正周期为π.
=π.即f (x) 的最小正周期为π.(2)∵f (θ)=
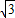 ,∴
,∴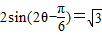 ,∴
,∴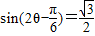 .
.∵0<θ<
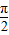 ,∴
,∴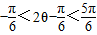 ,∴
,∴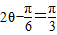 或
或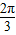 .
.解得
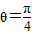 或
或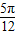 .
.∴当
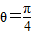 时,
时,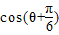 =
=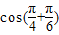 =
=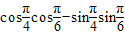 =
=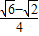 ;
;当
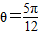 时,
时,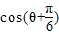 =
=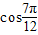 =-
=-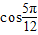 =
=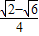 .
.点评:熟练掌握三角函数的单调性、倍角公式、两角和差的正弦余弦公式、周期公式、向量的数量积是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
设向量
=(cos2x,sin2x),
=(cos2x,-sin2x),函数f(x)=
•
,则函数f(x)的图象( )
| a |
| b |
| a |
| b |
| A、关于点(π,0)中心对称 | ||
B、关于点(
| ||
C、关于点(
| ||
| D、关于点(0,0)中心对称 |