题目内容
(本小题满分12分)
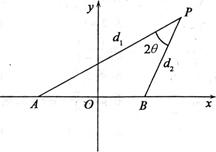
设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,
∠APB=2θ,且存在常数λ(0<λ<1=,使得d1d2 sin2θ=λ.
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)过点B作直线交双曲线C的右支于M、N两
点,试确定λ的范围,使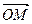 ·
·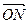 =0,其中点
=0,其中点
O为坐标原点.
设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,
∠APB=2θ,且存在常数λ(0<λ<1=,使得d1d2 sin2θ=λ.
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)过点B作直线交双曲线C的右支于M、N两
点,试确定λ的范围,使
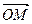 ·
·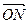 =0,其中点
=0,其中点O为坐标原点.

(1)动点P的轨迹C为双曲线,方程为: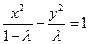
(2)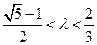 .由①②知
.由①②知
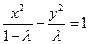
(2)
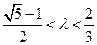 .由①②知
.由①②知
解法一:(1)在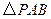 中,
中,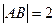 ,即
,即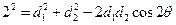 ,
,
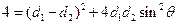 ,即
,即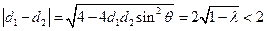 (常数),
(常数),
点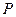 的轨迹
的轨迹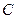 是以
是以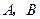 为焦点,实轴长
为焦点,实轴长 的双曲线.
的双曲线.
方程为: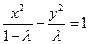 .
.
(2)设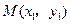 ,
,
①当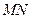 垂直于
垂直于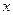 轴时,
轴时,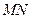 的方程为
的方程为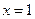 ,
,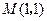 ,
,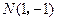 在双曲线上.
在双曲线上.
即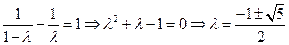 ,因为
,因为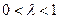 ,所以
,所以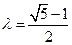 .
.
②当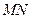 不垂直于
不垂直于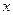 轴时,设
轴时,设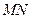 的方程为
的方程为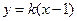 .
.
由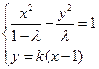 得:
得: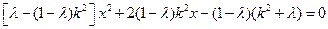 ,
,
由题意知: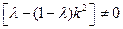 ,
,
所以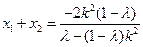 ,
,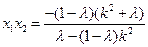 .
.
于是: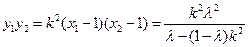 .
.
因为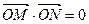 ,且
,且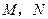 在双曲线右支上,所以
在双曲线右支上,所以
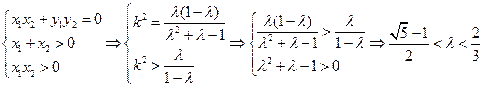 .
.
由①②知, .
.
解法二:(1)同解法一
(2)设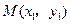 ,
, ,
,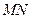 的中点为
的中点为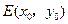 .
.
①当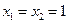 时,
时,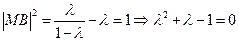 ,
,
因为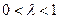 ,所以
,所以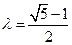 ;
;
②当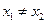 时,
时,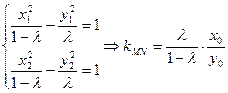 .
.
又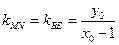 .所以
.所以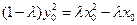 ;
;
由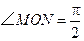 得
得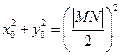 ,由第二定义得
,由第二定义得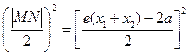
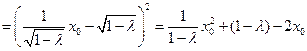 .
.
所以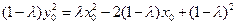 .
.
于是由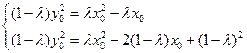 得
得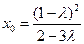
因为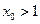 ,所以
,所以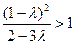 ,又
,又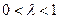 ,
,
解得: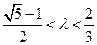 .由①②知
.由①②知 .
.
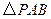 中,
中,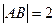 ,即
,即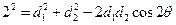 ,
,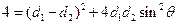 ,即
,即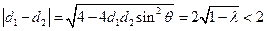 (常数),
(常数),点
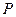 的轨迹
的轨迹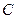 是以
是以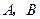 为焦点,实轴长
为焦点,实轴长 的双曲线.
的双曲线.方程为:
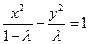 .
.(2)设
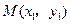 ,
,
①当
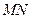 垂直于
垂直于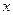 轴时,
轴时,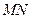 的方程为
的方程为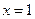 ,
,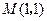 ,
,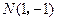 在双曲线上.
在双曲线上.即
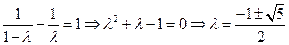 ,因为
,因为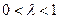 ,所以
,所以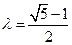 .
.②当
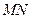 不垂直于
不垂直于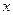 轴时,设
轴时,设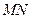 的方程为
的方程为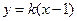 .
.由
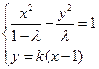 得:
得: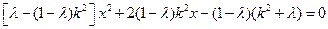 ,
,由题意知:
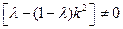 ,
,所以
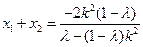 ,
,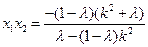 .
.于是:
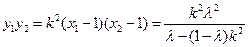 .
.因为
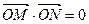 ,且
,且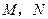 在双曲线右支上,所以
在双曲线右支上,所以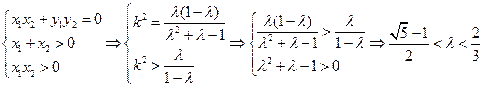 .
.由①②知,
 .
.解法二:(1)同解法一
(2)设
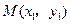 ,
, ,
,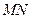 的中点为
的中点为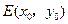 .
.①当
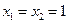 时,
时,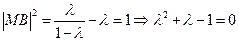 ,
,因为
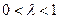 ,所以
,所以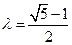 ;
;②当
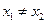 时,
时,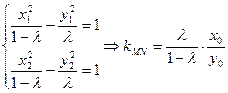 .
.又
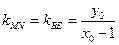 .所以
.所以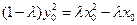 ;
;由
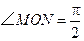 得
得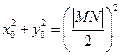 ,由第二定义得
,由第二定义得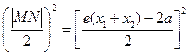
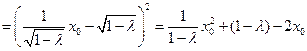 .
.所以
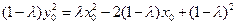 .
.于是由
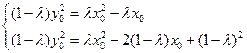 得
得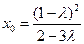
因为
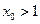 ,所以
,所以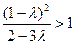 ,又
,又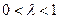 ,
,解得:
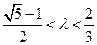 .由①②知
.由①②知 .
.
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
 和
和 分别表示椭轨道Ⅰ和Ⅱ的焦距,用
分别表示椭轨道Ⅰ和Ⅱ的焦距,用 和
和
 ②
② ③
③ <
< ④
④
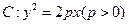 的焦点为
的焦点为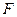 ,
,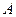 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于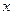 轴上方的点.
轴上方的点. 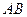 垂直于
垂直于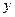 轴,垂足为
轴,垂足为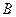 ,
,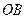 的中点为
的中点为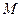 (
(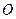 为坐标原点).
为坐标原点).
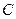 的方程;
的方程;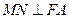 ,垂足为
,垂足为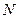 ,求点
,求点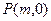 是
是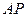 与圆
与圆
 ,(
,( )的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点
)的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点 ,求抛物线和双曲线的方程.
,求抛物线和双曲线的方程.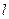 :
: 过抛物线
过抛物线 的焦点.
的焦点. ,若
,若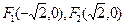 ,平面上动点
,平面上动点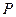 满足
满足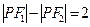 .
.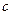 的方程;
的方程;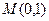 的直线
的直线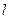 与
与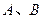 两点,且
两点,且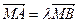 ,当
,当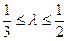 时,求直线
时,求直线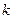 的取值范围.
的取值范围. ,直线
,直线 :
: ,
, 为平面上的动点,过点
为平面上的动点,过点 ,且
,且 .
. 的方程;
的方程; 过定点
过定点 ,圆心
,圆心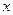 轴交于
轴交于 、
、 两点,设
两点,设 ,
, ,求
,求 的最大值.
的最大值.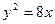 的焦点与双曲线
的焦点与双曲线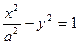 的一个焦点重合,则该双曲线的离心率为 ( )
的一个焦点重合,则该双曲线的离心率为 ( )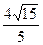
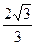

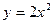 ,点
,点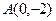 及点
及点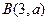 ,从A点观察点B,要使视线不被曲线C挡住,则实数a的取值范围是( )
,从A点观察点B,要使视线不被曲线C挡住,则实数a的取值范围是( )


