题目内容
(本小题满分13分)已知两定点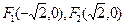 ,平面上动点
,平面上动点 满足
满足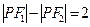 .
.
(Ⅰ)求动点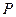 的轨迹
的轨迹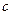 的方程;
的方程;
(Ⅱ)过点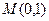 的直线
的直线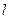 与
与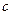 交于
交于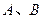 两点,且
两点,且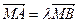 ,当
,当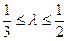 时,求直线
时,求直线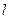 的斜率
的斜率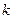 的取值范围.
的取值范围.
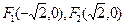 ,平面上动点
,平面上动点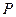 满足
满足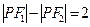 .
.(Ⅰ)求动点
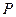 的轨迹
的轨迹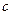 的方程;
的方程;(Ⅱ)过点
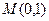 的直线
的直线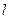 与
与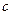 交于
交于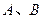 两点,且
两点,且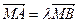 ,当
,当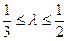 时,求直线
时,求直线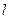 的斜率
的斜率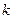 的取值范围.
的取值范围.(Ⅰ)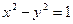
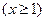 .
.
(Ⅱ)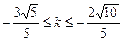
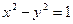
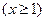 .
.(Ⅱ)
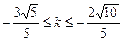
(Ⅰ)∵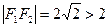
∴ 的轨迹
的轨迹 是以
是以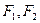 为焦点,实轴长为2的双曲线的右支,
为焦点,实轴长为2的双曲线的右支,
∴轨迹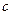 方程为
方程为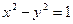
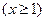 . (3分)
. (3分)
(Ⅱ)由题意可知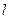 的斜率
的斜率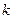 存在,且
存在,且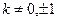 ,
,
设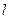 的方程为
的方程为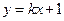 ,
,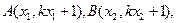
则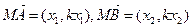 ,由
,由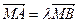 得:
得: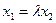 ; (5分)
; (5分)
联立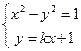 ,消去
,消去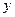 ,整理得:
,整理得: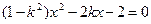 (*)
(*)
由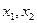 是方程(*)在区间
是方程(*)在区间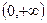 内的两个不等实根得
内的两个不等实根得
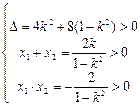 ,化简得
,化简得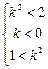 ,即
,即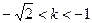 ; (8分)
; (8分)
又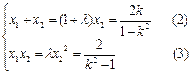 ,
,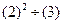 整理可得:
整理可得:
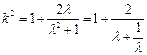 , (10分)
, (10分)
∵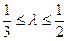 ,由对勾函数的性质可知,在区间
,由对勾函数的性质可知,在区间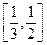 上
上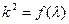 为增函数,
为增函数,
∴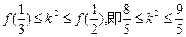 ,
,
综上得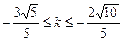 . (13分)
. (13分)
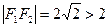
∴
 的轨迹
的轨迹 是以
是以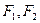 为焦点,实轴长为2的双曲线的右支,
为焦点,实轴长为2的双曲线的右支,∴轨迹
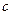 方程为
方程为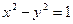
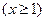 . (3分)
. (3分)(Ⅱ)由题意可知
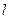 的斜率
的斜率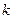 存在,且
存在,且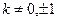 ,
,设
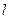 的方程为
的方程为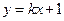 ,
,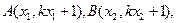
则
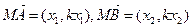 ,由
,由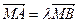 得:
得: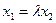 ; (5分)
; (5分)联立
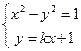 ,消去
,消去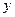 ,整理得:
,整理得: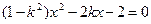 (*)
(*)由
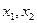 是方程(*)在区间
是方程(*)在区间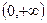 内的两个不等实根得
内的两个不等实根得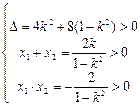 ,化简得
,化简得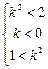 ,即
,即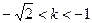 ; (8分)
; (8分)又
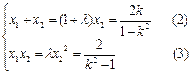 ,
,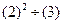 整理可得:
整理可得: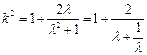 , (10分)
, (10分)∵
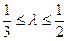 ,由对勾函数的性质可知,在区间
,由对勾函数的性质可知,在区间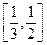 上
上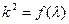 为增函数,
为增函数,∴
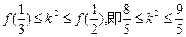 ,
, 综上得
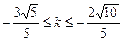 . (13分)
. (13分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ·
· =0,其中点
=0,其中点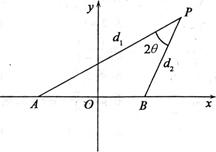
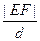 的最大值.并求出此时b的值
的最大值.并求出此时b的值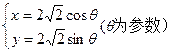 交
交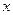 轴于A、B两点,曲线C是以AB为长轴,离心率
轴于A、B两点,曲线C是以AB为长轴,离心率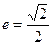 的椭圆。
的椭圆。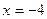 上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且
上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且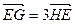 。试求此时弦PQ的长。
。试求此时弦PQ的长。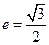 .直线
.直线 :
: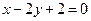 与椭圆C相交于
与椭圆C相交于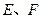 两点, 且
两点, 且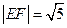
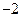 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当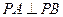 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.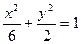 和双曲线
和双曲线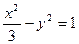 的公共焦点为
的公共焦点为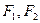 ,
,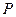 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos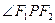 的值等于( )
的值等于( )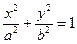 (a > b > 0) 且满足a≤
(a > b > 0) 且满足a≤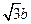 ,若离心率为e,则e2 +
,若离心率为e,则e2 + 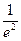 的最小值为 。
的最小值为 。 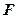 的直线l与抛物线C相交于A,B两点。若AB的中点为
的直线l与抛物线C相交于A,B两点。若AB的中点为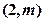 ,则弦
,则弦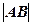 的长为_________。
的长为_________。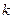 ,那么甲的面积是乙的面积的
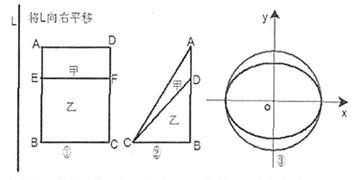
,那么甲的面积是乙的面积的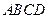 、乙:小矩形
、乙:小矩形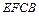 )、②(甲
)、②(甲 :大直角三角形
:大直角三角形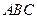 乙:小直角三角形
乙:小直角三角形 )中体会这个原理,现在图③中的曲线分别是
)中体会这个原理,现在图③中的曲线分别是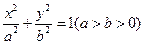 与
与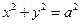 ,运用上面的原理,图③中椭圆的面积为 .
,运用上面的原理,图③中椭圆的面积为 .