题目内容
13.若函数y=cos2ωx-sin2ωx(ω>0)的最小正周期是π,则ω=1.分析 利用二倍角的余弦公式化简函数的解析式,再利用余弦函数的周期性求得ω的值.
解答 解:∵函数y=cos2ωx-sin2ωx=cos2ωx(ω>0)的最小正周期是π,
则$\frac{2π}{2ω}$=π,求得ω=1,
故答案为:1.
点评 本题主要考查二倍角的余弦公式的应用,余弦函数的周期性及其求法,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.已知在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$中,F1,F2分别是左右焦点,A1,A2,B1,B2分别为双曲线的实轴与虚轴端点,若以A1A2为直径的圆总在菱形F1B1F2B2的内部,则此双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$离心率的取值范围是( )
| A. | $(1,\frac{{1+\sqrt{5}}}{2})$ | B. | [$\frac{1+\sqrt{5}}{2}$,+∞) | C. | $(1,\frac{{1+\sqrt{3}}}{2})$ | D. | $(\frac{{1+\sqrt{3}}}{2},+∞)$ |
18.已知直线x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)图象的一条对称轴,则y=f(x)取得最小值时x的集合为( )
| A. | {x|x=$\frac{7π}{12}$+kπ,k∈Z} | B. | {x|x=$\frac{11π}{12}$+kπ,k∈Z} | C. | {x|x=$\frac{2π}{3}$+kπ,k∈Z} | D. | {x|x=$\frac{5π}{6}$+kπ,k∈Z} |
2.等比数列{an}中,a3=16,a5=4,则a7=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | $\frac{1}{4}$ |
3.若复数z满足(1+2i)•z=|2-i|,则$\overline{z}$( )
| A. | 1+2i | B. | $\sqrt{5}$(1-2i) | C. | $\frac{\sqrt{5}}{5}$(1+2i) | D. | $\frac{\sqrt{5}}{5}$(1-2i) |
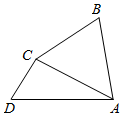 如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).
如图四边形ABCD,a,b,c为△ABC的内角A,B,C的对边,且满足b(1+cosA)=a(2-cosB).