题目内容
如图，三棱柱A1B1C1-ABC中，侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC中点，则下列叙述正确的是（ ）| A、CC1与B1E是异面直线 | B、直线AC⊥平面ABB1A1 | C、直线A1C1与平面AB1E不相交 | D、∠B1EB是二面角B1-AE-B的平面角 |
分析：由题意，此几何体是一个直三棱柱，且其底面是正三角形，E是中点，由这些条件对四个选项逐一判断得出正确选项．
解答：解：A不正确，因为CC1与B1E在同一个侧面中，故不是异面直线；
B不正确，由题意知，上底面ABC是一个正三角形，故不可能存在AC⊥平面ABB1A1；
C不正确，因为A1C1所在的平面与平面AB1E相交，且A1C1与交线有公共点，故不正确；
D正确，因为AE⊥侧面B1C1CB，故∠B1EB是二面角B1-AE-B的平面角正确．
故选：D．
B不正确，由题意知，上底面ABC是一个正三角形，故不可能存在AC⊥平面ABB1A1；
C不正确，因为A1C1所在的平面与平面AB1E相交，且A1C1与交线有公共点，故不正确；
D正确，因为AE⊥侧面B1C1CB，故∠B1EB是二面角B1-AE-B的平面角正确．
故选：D．
点评：本题考查空间中直线与平面之间的位置关系，解题的关键是理解清楚题设条件，根据所学的定理，定义对所面对的问题进行证明得出结论，本题考查空间想像能力以及推理谁的能力，综合性较强．
练习册系列答案
相关题目
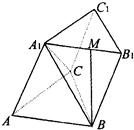如图，三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧面ABB1A1是菱形且垂直于底面，∠A1AB=60°，M是A1B1的中点．
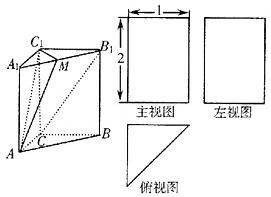如图，三棱柱A1B1C1-ABC的三视图中，主视图和左视图是全等的矩形，俯视图是等腰直角三角形，已知点M式A1B1的中点．
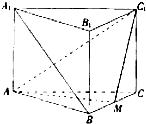如图，三棱柱ABC-A1B1C1中，侧棱与底面垂直，AB=BC=2AA1，∠ABC=90°，M是BC中点．
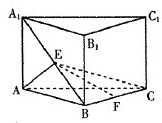如图，三棱柱ABC-A1B1 C1中，侧棱AA1⊥平面ABC，AB=BC=AA1=2，AC=2
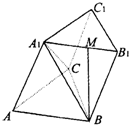如图，三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧面ABB1A1是菱形且垂直于底面，∠A1AB=60°，M是A1B1的中点．